Orbit prediction for Aeolus
Contents
Orbit prediction for Aeolus¶
Authors: Alexander Geiss
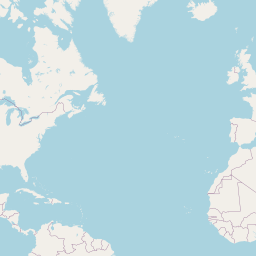
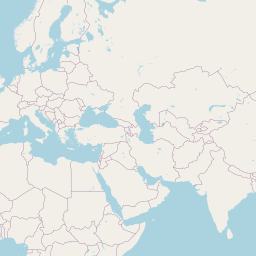
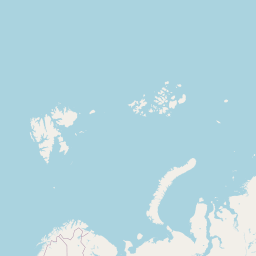
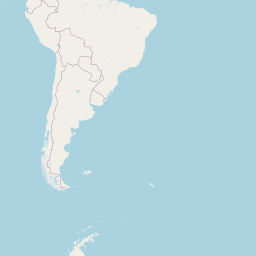
Abstract: Using orbit ground track files (
GRND_TRACK) to predict Aeolus overpass locations and times
Load packages, modules and extensions¶
%load_ext watermark
%watermark -i -v -p viresclient,pandas,xarray,matplotlib
Python implementation: CPython
Python version : 3.9.7
IPython version : 8.0.1
viresclient: 0.11.0
pandas : 1.4.1
xarray : 0.21.1
matplotlib : 3.5.1
from viresclient import AeolusRequest
import numpy as np
import pandas as pd
import datetime as dt
import os
from ftplib import FTP
import tarfile
import fnmatch
import math
import getpass
from base64 import b64decode
import ipywidgets as widgets
from ipyleaflet import (
Map,
Marker,
LayersControl,
MeasureControl,
)
request = AeolusRequest()
About orbit ground track files¶
Orbit ground track files are produced once per day to compute the AUX_MET files which contain ECMWF model variables and are necessary for processing the L2B wind product.
Among other variables, these files include predicted geolocations from off-nadir (right-most swath point) and nadir (ground-track) intersections (see Fig. 1) with the Earth surface (WGS84) for one week.
Geolocations are saved in steps of 3 seconds. Because the orbit repeat cycle of Aeolus is 7 days, all possible orbits are covered with one GRND_TRACK file.
Since orbit ground track files are ASCII-files, they are easy to read an can be used to estimate overpass times for ground stations or whole regions in case of airborne campaigns.
Since the mission requirement for the accuracy of the position of the reference orbit is +/- 25 km, one should always use the latest file if high accuracy is required.
Otherwise it is sufficient to use any file within a period of the reference orbit. Once a week, so far on Thursdays between 13:30 and 14:30 UTC, so-called OCMs (Orbit Correction Maneuver) are performed, which may lead to strong deviations between the actual orbit and the prediction.
There were two different orbit periods for Aeolus, one with ANX 4.5 and one with ANX 2.0. ANX is the ascending node crossing at the equator and is specified as a longitude offset from the prime meridian at the equator in positive values toward the east. It is given for the first orbit east of the prime meridian at the equator.
ANX periods for the Aeolus mission:
Date |
ANX |
|---|---|
mission start - 17th June 2021 |
4.5 |
17th June 2021 - 21st June 2021 |
drift |
21st June 2021 - today |
2.0 |
Aeolus measurement geometry¶
aeolus_meas_geometry_encoded = b"iVBORw0KGgoAAAANSUhEUgAAAtAAAAHYCAYAAAET6+/6AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAP+lSURBVHhe7J0FYBTHF8avpU6dtv8KFGhLoS1S3F2KFHcKhVJKaaEUiru7u7slkBDcg7sFS4BAcIcIIS58//lmd8kR4rlL7pL5tcvNyu3tbea+ffPmzRsTFCnCCzc6NDRUvg4bNgyRkZHo168fwsLCMHToUCxbtgxbtmzBrVu35DEGbm5u6N69O27cuIErV67g6tWrcjvXSeXKlTF37lyMHTsWo0ePltvSG8mq0WfOnNFLCadPnz56KX3xwo2eNWsWChYsiIiICH0LsHbtWr0UxeLFi7F9+3Y0atQIM2bMwJMnT/DXX3+hc+fO+hHA66+/jvfeew8ffvihviX9EmuN9vb21ktRhISEyNchQ4bIVwNjO7l586ZeAsLDw/WSItYbzRq9Y8cOWV6zZg1cXV3x9OlTuU4N9vLyktpt3Fjj2ODgYOzcuVOWefz169fx8ccfS+12d3eXS3okWRqtSDgWudG7++/SSxqz8s6Sr5ERkVjXei3CAsPg6+Ujt6VX5I0ODw7HmSVncGXHFVzefEnuiAzTHoY+l7zhNtcNIf4h8NzgCR9xw3yv+Mp9TyM1Kbm+9zruud2TZc8NFxH6JBQeTh5y3WOlOwLuByDwQaC88Z7rPOX2a3uuydf0Qqw1enb+WXD4eQVm/DADC0svxPGZxzG30Bxsbr8ZF9ddxOJyi+RxvHlXtnvJ8qa/N4o/yklMzjZJrpMDI/fDa5sX5heZp29JnyiNTiHUjU4h1I1OIezqRrM1aq/YxY0uWbKkXgKaNWuml+wLJR0phM3f6JkzZ+ol4IMPPpCvjx49kq/2hKrRKYTd3Og2bdroJfvELms0PYT2ht1Kh3Gzbx2+hV19d2Lf0H24e/IuZnw/HfMKz0VkWCSWVloqj7EF7Fqj2adpL6iHYQqhbnQKkSZu9J49e/SS7WLXN/rUfDfs6LodkaERMJls+6so6Ugh7OpGn5h5/Lnemw1t1usl20fV6BRC3egUwqZv9BwP4JftwMMgfUMCOX3KDV3PhqG5FtNjE1j8Rns9Fi22p+LEU4FP5gNlVus7YsHdG2i/V1+xMDGFpDFAot1urZySJPlGDzmuvT4MBqqu024qcdDCNmJkljtwWfwhbI2Bx/SCFUnQjeZP9+VpQOaF+gZBl/3A/TicaEfuATufD6NOFRgfmFh+c9ULFiTeG/2FuLlfLdFXYsEvFOh1SF9JYRh3GRIVYRwjmzZtwnkPLXIqKbR+PuItSSRaOm4GAP/u01esBH1yNTcBV/21dUvQ8xJQzQJmN6/pURLc4XHeaLeH8deWmBh9UnvlAzG7+DW0jaNGlFurPaBSi2bCqkkOrbUI5XhJ8sOQFHfSXn1DgN1Cj42a3u+I9hqdWqKW2joOoubrsZtJov4WvRCNBN/oMPF7zusg3jARuBeo/bwnn9b2xUTdzXrBgljCcZRYT19ya7xBgq98zRW9EAMjhVTQzLMWAwcOxN9//y00JmGX26RZU3h02YTJWSdhUpaJOPK3I3z7R/3MkvMHG6abtYkl0Z/YUPw0gqwwNGXRokVYuXKlvpY8Gsx+/msdOxZlKPtc9kbRz4vhq4+y6FuSzr47QGgCn2FJ/9PGwZH7QFkX8aAQ9qi/MP0uiUbKRd+oi6pXr55WSCDZsn4imnkJu9RtW3dgfNjzxz4Jf4gSOd7S1zS66a8GHBy1eXPy9O7XOOzvZN9oSgp/Ti9PB97Ug4qmmQ0//O23354bSpcUKlV4BYnph/2pUza9pPFtoQ/hP+r5r9pDLD/++6+2EgN37tzBxYsX9bWkwdZzuH7dCb7RoeINNNf0gVl4ZQbwTzQfxZIlS+RoLUtTvVrC68Ojhy8O2yNLm754jqrzFuil+OnWLfpvIHHE+w0eCAvj9CNhUz/QN+hQU48ePaqvWZOE32RSumPMx58Pitnuqjh7rl5KHH/++adeShgJ+ha//vqrXkpZOv7TVfybuNFck+L4SuvbvLgvZ9u2einpcKzl3bt39bWYSVx1SWH++D3xl1fqn9jf82h4zPuSJwovwsGvDx+KZrUZNn2jk0QcrbqV9/7RS89zTM/oYE1S5Ua79KsEv5sZEez7Gg4syY2VvSpg38I8cOxRUew1yXXfm2/D++o7cOxZ8dn66oFlMb5NYeT7Iafctkrs++jBG/jw4evy1Vm830ksq3pWwOIBZdFoS3a5nccaNP1R+8rLljvAsXdFNNs0GybxoHfoXQkvCROh6Za5WNWrPD5+dBeTxrSQN2jBoFri2Eq4d08bS5kUUu1G+1x/BweX5YbLgDLiZlaAx45s8tXnxjvyxjj3K4crRz7DedeseHTtXTy8/J7cb36jeRO5jJtQVN5gbhs+taC4KeWxSPxR2jjlfLb9GdOjbjS3zxjRWPyBysryrOENxR+oBpb2qyrXZw+rjxV9KssyF7u70cmFN7qN87foLn4F8weXxtwhpcVNKYUxE4tgdfeKKHA2k6zN67pUxtt+r6LJ5uz6O4EOm76Tr7zRq3qWR+/5PTB3aF04dy8r1517lJGvvDGru5fB6El/4Nf10/HeY5/0eaMd+pYXP/EKmC9u8ryhpWXZoY+2jcsy8Yswti3rX05/p0ahH7Ji6bLlmPJnEbEU1V+Nsvlivq1IvJZFXNjljU4201L+a6fLG13499f0UsqRPmt0KpCmb3R4RMQzi8FYHIRJiCkm7B+YB/fGfPDC/uEjRunvtizp7kbHt6gbnQR4oyMmvYydAwpgU9+iODjoBzj2qojgCa/Lmxo28RX5en3UJ/AYnhWYbFI3Oqkw8WFiFvPeGEuiHoYpxAs3mjntPD090atXL5w8qQVo/PTTT7h9+7ZMJDh+/HiZ/nLw4MFy3yeffCJfozNu3DjZS/HHH3/A398/xjx66Ykk12j+zBIKc5qS5HZp2TMv3OgMGTKgVq1a+N///ofvv/8ehQsXltuNGsybxTZ/hw4d5Dpp3769vPE1atTAiRMnULFiRWTJkgX//PMPWrduLZMLkvLly8vX9EiyNPrBg2j9WwnAPKVmeuK5Gx0QECB7B5jcleWY8mIcPnxYJnxlDAZTIAcFBUktJqzNRspjnocwkvPSpUsy9THTZdatW1duT28kq0YrEo680czE+OTuE5xZcho7euyA/y1/HBp7EFs6agElTyNi7x9yX3FWLyni4lmNPjHzhHw9OfskAh8G4tquazJDI7MwRgRrMWBMf+l71RenF2nRjfzDeK73RLBvMM4ueTFp96FxB3HnxB2ZdZeL3zU/uf3WwZt4fCNxYyxatWqll+yTWKXj0cVHmP7tNJl/dGsnLSbi9tHb8tWAeTGYTnNazqly/fiMY5hbSIuT2NhuI7b/tw2rmznDa2vyg2oM68desRuNzps3r16yT+zmRhcqVEgv2Sd2c6NLly6tl+wTu7nRxYoV00v2id3c6Dp16ugl+8Smb/TBgwf1EtCkSRO9ZJ/YTY3+/fff9RJkk97esPkbbUxJQg8hfdv2il3U6GrVqqFnz576mn1iN9IxcuRIvQQcOHBAL9kPdnOjzdMbm/PkzhMsLL1ApsqMDI+Ec2Mn6QSbnmsaFpbSxqgY05mkJnZzox0cHPSSfWI3N5rzKEbnl19+0Uu2j93c6CNHjugl+8RubnRyB1emNnZzo+/fv6+XgLPLzmJp5aVYVV8bOz75y6ikg7aK3dxoH5+Yxxsem5oCmacsgN3caEY7mddcziYXHU67GhPGZMOpid3caIY1JAQG7EQn+o2uXbu2Xko57OZGJyWtWmykRmyJ1W90UpOoMLVQ5XXAkmfGRsITHfX0BGo53MNuvS/ZCElLTSx6o3sfAm4HaGW+vj4dGOemrccGcxb5WCFNkHn0qrl0dDkAVK+Z8p0IybrRI04A228ALfVkq3XiyALGzFs1NugrqUx06Ygtq5klifdG196ovTL3KG+swTfxZHesZiM39fjx44m2OlZe1gsWJN4b/bY2IXKctNkFhCdcQi0K8zTFlwSRc5Obk5j+RxcLyXuipeMPcVOZizQxXElkht0Vl4AeFsx12tsLmHA26qYlp6O3ahLTbsZ5o6Oe+Amn0RZgoz4T9QNh+n4sJKfvYW09OluEvq9Kge4/SkdMnbvMQDnrnL6SBPjcYebHhJCshyGpJTR8q/hl5l6hra+OJcyOusdcp6mBodFsXZK47OimycjcyOSwsX3/BN1o0xTtNb8jUFN/OJIeUdEAz8Hg07Gn9BUL8corr+il+Gmcp5peipnESMcmC80TH++Nvh8I5NLG+sQIQ6cbxJyAyyKcP39ejql5msAEg6Rk7iJauswvJ2JO1dnAqIvI82UuuY/pMr/66itZTizj42kTxEWipOPUI2BAEjKwDT0GbBY144M5+oZohISEyCF2cfG/T5KtcpJ9w/aJG38Bzs7O+pak03ibXkgAlrl6M/SYdXQW36eDntjWsL9niAfPuXPnsGBBwhP7SURtLlToVX0lbiaIY78poM1N+4zJL37N3CVK6CWN+vXr66WkwYyNtJZiI0k32kgDSZiW/hXR1CYB0fw+HFQ0YMAAfS3pjBllQnh4wtKw/3fyxa+UPb8J20P762sanUPC4pwPsXr16nop6fxtluky3ht9URsNgf/2a69Mk0k7Outi0RB4om0zoJZaGp+HiasLsSUYLFsyWjTq06fIXCjhowhmzUpAyy0O4v0WtwKA75a/6DurUqWKXrIerHE+Pon7nC8KxvKVpr64/eMkDtdYvTqeyWViIN4bzaf+qVMWttUSSGIsDYMnkVF9i+Z8VSXmc/0bmHzXYYUKZuneYiHx3ySF+L1V4i/t+8JxJ98eOWa8Xoqil5flPUiVKlXSS1HY7I22CrFkBxsmzEtrkyo3ev3wElg7pBQeXH4Pj29nxMV9mbF1QhEEPHoNIX6vwqF7RfjeeAdB3q/jvucHcN+WDWc2fQWXgWXl+5k1ZsTkwjJF5u+rc+J/d998ljIz+9V3ZPn7i+9r28S5VvXWftr5ckZ9XZ6DWRtzep3BjJGN4dSjHOYPrg2HPpVQ/shmLOtXFS9FAO2cRuP3NZPk8ckhVW40L3rd8FK4uCeLTIV5euPX2Di6OLwOfo5Dy36Q+5mn1FHcJL5uGlsMh5f/AA/XrM/eP2xqIZl/9J/l32vH9y4vbu4HmDO0FDI9eB3v+L4ic5Ryn3Gjn4r/bt7WkgRy+0qxf96QuuI99bR1fWFuUuYqdepZTmZ1XNK/mtyeHOxSOt7zfg2vP3kZLt0qiS8g/hMPzbrbs4qbUhFTxB/sPZ/X4NK9kkybOWt4SZn10SBsovaV2zqPxaCZ/2L2sHr4yPseip3ejUzilWkyR03+Ex/4PkSfud3wckSEvNm8+cnBLm+0kRpzsZASvjJt5tIBWopMLitFDTbKXJz0Gk0G/6R95RfTYsafNjM52OWNTg4PwuOYB9CKpLsbTXKWSPmvnS5vdGqQpm+0uSVhLJ4jMsNtyDcx7uNiLdLdjY5vsRZp/EYLO1wsT8a/Af/xb2LPwHx4OsmEjX2LI3TiK9JP/Wjsu7g/5gN5nLrRScQ8FWZCF2uhHoaKNEW8FTp6WPKFCxewdu1aNG/eXKYqXbVqldz+8ccfy9FoGTNmRNeuXaWncP/+/TKfIIdzHzp0SKbJ4+Cqtm3byv5YwnGavXv3linxmGZv8uTJMgyDx3Ld19dXJo5k2chNyIGzTJtarpw2RwLd5UwemT9/frnO1KqEqfuYTFKRfrCIQrOCxpXe1chPYD6uKikEB7/YF/L222/rJYUiGRWawRlUT1sme/ao6YQU6YM4KzQjLllpaVps2LBBBsO0bNlSZkZnmYPgaRqQ06dP499//4Wfnx88PDwQHh4uj+ErlXXo0KFYs2YNxo4d+2yqVGbl5bm3bt0KR0dH+V6+h2YOP5dmCc2LpUuXSlOE76faP378+JkpxFky33jjDbkwpIwm0VtvvSXjS7gwPVBsGdsVaQ/VKFSkKVSFVqQpnqvQV3Zo45UeeWijTEKfaOYEs0EtqbgYD87cx6mFblhUbqHcvuGP9dg/bB82d9iMCy4XsOnvTYiMiERYYBj2Dtojs0YdmXIEx6YexRXXqzjvfB6XN1+SGb0ZLsmk1OTUfDfs6L4Dnusu4vTCUzjncA7nVpzF0clH4OHkIfZth98VP7j2csW0b7Uk1Uxi7b7SQ37Gml9dsLjcIrn93ql78Lmk5ZpYUX05pubQB4QITs4+gW2dtuLwhFiGLSnsniQrtI+Xj1Yx48HncjwTp0ePA04GEfGN6EwhSkQbRaBIORJdoecVnYsQUZGp2kzdP7/IPIQ8DsHSSksQGhgq1ZQsKb9YvhpwPTIsUlNS3Y23pMJiRIRGyLRIVOJVDTSfNrl58Kacy8FgURntqXBsylEsq7JUlmflm4XZ+Wdhq1Bdt7kn5XwPC0rMl/tSE8Mfrkh5lA1tBX788Ue9pEhpVIW2AvY+CYE9oyq0FUjPczWmNqpCWxiO3+fkpKRUqVLyVZFyqAqdTDg/dHQaNmyolzQYJqBIGVSFNoNJljiJ7q5du+TkuFTbJUuWYM6cObLrffTo0XL66D59+siIQgZGcTKYFi1aoFGjRrKrnd3vzENUtmxZOSi8cuXKqFq1qow+ZLZZ5hViMhAe37RpU/z2229o164dOnXqJCdfHzRoEEaNGoVJkybJFAqLFy+WYQGKhKEqtAVg/Ik5jC8xJ73OFJ0aqAptIYxpzwnVmzHcJHfu3PJVkTKoCm0FBg4cqJei4Fx1CuujKrQVmDhxol56npgSUd06fEu+ciKZS5su4fqe6wj1D8WDcw/kdnbn33W7i1l59BnYngI39l6H15bLMn7G77ofPFZ5wP+OPy6ute8ZgCyBqtBWYOFCrZs+Nl566SW9lDwYrMXpAxVRqAptBTgQISHElZ1TkTRUhbYCe/boCYUTwJdffqmXFJZAVWgrwOFoiWX6dD0JtCJZqAptBYyJdPYO1jJyuzu6y1fCsFtzGHqrsByqQlsB5hBJCCvrOsrpcVnJp2SbjIgwbYBCyZIl5asi8agKbQU4ej2hPL4Z83Rh7PpOLImdyy4toiq0FWDGJoMNbZI4J5wVSA9d8KpCWwEjzZmlYB4Uoys9LpRCqwptHZ5GDdbljNxnvYH114ApZ4Ahx4Eu+4G/9kQtXQ8Cw04ACy+IhuQd4NaT52fCIhFhYXgpw6vo3bMHIsJjngY9vgqdGnPLpzR2V6HXi79ZoPh7frk4aiLst5I3UVWMcKYvzvxVZR2w+fnZf1OFY8eOYWC/vmhQv/6zuUSj43oLqLAWmBDLVE/K5EhFvhIV9p3ZQsF2A556G6vpNmCFJ/CmqMA7xR8vtglcY2Oeh6igwqTdI1TQ3smTJ49eiiKhJgen56u9CVieOhNHWJUUrdCc4/CJ/rTk/NknHgAZReV8LG4wZ+5kZV0gKl1iWSwe1Zw53yuR84unBUqXLq2X4q/QiVHoUSeB/kf0FTvCIhX6hng8fzhXK/8tbMLsS56vXD5JnBHwmniyNtoKzElCJU9PBAUF6aW4sZTJ4SPavLYqIKlicgSJNtN/B7QGEW9OWuCq+PFNOg38sh1o5gqMdgNOPQT8Y26/JQkG1nGG3+nnxGcI86uFaEMsFU81PuFyVG2EmmNXoNmSfSjQuofM0Jpa/LYTcNGyyqU4Fq3QS8TNZSPKKZG2bVLoJn4QZK5Qb04wHip+JC9N07YlB19ROQYeBRqIJ8OR5OVnT1FOnDjxbIYDjn2MDoUjZ9m66Lxf87ykFvwxdj+or1gBm2wUhpq5rDhxezkXoUBLgYPaxJnIvUIzbbIs1P44CYkIZgPoZ/GYdNPyUKZ5YqrUCTE5KBCtxBMmNcKsfcWPrs5mYPdtfUMSSPEKzRBgVlBePGkslPBmgLiQKZo7jiTGDDn9CKiwRnPnpXdiahTOmzdPL1mG4SfEE+yYvpIKUN3/FU8ZPXHtC1ikQhfQR9kvPA+8rD/2vxaK+vZMzSdqPOL0HI0JIkJUfD4e/9YC1uwCBuyvW7cRhQsXww8/fI+1aze+EMTPuWho3545cwa7d++Gi4sLli1bJhfOVMAJmfbu3YtLly7J2RGM+Wl2/rEIGHUBGH8NI8eMlNuiU6VCZb30IiaT6YV8IZaGjfhKwuSk+ZdapLhCB4rKPVj8whtsAe5GJRe1aTj9xcaNG2U+jW7duuHGjRv6nhdhRd28eQf27DmEnTt36Vuti99VP4ypOgYrGo9D8LDTmJxtEiZ+MQHTvpmK9W3WY7/rfgwfORyhw8/ihNtJuLmJFmsKw0r+03rtiWpNLFKh/UVDiq17ei0uJzzQLMk4XAL+EHUlmxCthuKHQdhd/P4crdxJNBLfnysap5e19Zjg1G9M9NK/f/8X8moklUuXriAyzIRfmllWJ34o8DXGi/Pu3iVucBz8XSr2z/3otffl6w8ffyVfDbZt2yYT5Fy+HMfNSgEGiIY4PUPJJcUVOibOeesFnTDxlB5zUvOYkLl6fDw7Ycjx+8B5HyCrlrT/OS5evIh69erJjEcpC1unJgzoa0KnTsX1bclnXfjf+KqMCblrmvB949j/XDOcRsipcbmUKvxiL6JBD7F0Efe36eEjz8yZuAgMDESzZs3kxE6pRbBQd7ooFwiTNj6sWqGXRRtVT+Uk7IKm94INQVJnE/CGsLdzLdPWY2vlDhs2DK1atYK3d7RfQCrj5cXGGG/lZLluaSaJc3sGRyWyiY1HEDd8minOwberRSWu5eAAS01OzBgTCkhCfhwpQbIrdHGnqEe7oaiEfmK6gJaKe9xut74xFtavXy/zwHGWWXujYIFvcP6cKVEN3sTQpHEz/LE+4X+mAn++ivO94z/eQTROu4lXa1ZEDnTg3zWuNoelsZpCM4a3TZs2+Pvvv585/NMa611MKFjQardQMjbEhCGrm+prCcOtqwktWvyqr8XO7eBgqdTrE5h2wdIwUSXFzJJY96+RpjFh06YP9bJ12Lp5B8YEJP5PdDBsqjQ9EoRQ6N89vVDcxsYx0nVJdU/sYAlVoZPArl0mRESs1tesR7bKJhRr8ZG+ljhy5DVhaLWE/3l/aPUbcjZvoa/ZPg8fPkT16tWxYsUKfYtGuqnQvRt8h+51c6X48mvZLPLzmR5s4IABVl+eIUzjkHEmrF23Qd+gsXTZ8hiv09LL3bt6nEIKk24qtEu/SkC4CS6DyuDctmwIePgGtk0sIret7CUaLqc+xvndX2Lv/LzYMr4obp75CH6330Kwz2tYM7g0No4uDvcdWeHcvywce1TEI693xVlNcOxZATtn5cf6ESVx51wmea5T675BZOhLsjy+TWH5+fl+yCnXuQybWgirelaEszhPtutvY3X3Svj8zluYO6Q0nMQ2x97lMXhGQcweVgo/XHgf2a+9jYx+r8j3vhxsQoVDn2PYtILiHBXk8cZ5V/WuID/LYMqVWi+YHsuWO8hjHXtXxLgJreHcvQxyep1Bfo/DGDi7E5b2q4p5Q+ripYhIeVzL9dPw7TV38Tnl8KsoD575D7ou6gennuXwsfc9uHQrBVMkxLWUx9+rRj27loSMgbQG6aZCVyhZABVKpPxSvKCWH9q8QltriV6hSZN8JpTK+ba+FlWhWSFZCc3fz23yPPq+6Pu53blHWVm5uRjb5bl6accb71UVOo3DCr26e0W86/sqlvctj6+vvIPsV9+WFWLMpMJYLJTfpD8tqu/JjAGz84uKUVG+p9GW7PK1y+LcouKwYlXAui6V5bF8D9dbu+SIsUJHssNHqPRjf603lBV63tA6mDW8oVDnsvj26jm8HeAvlTr7TU98+uAWip3eLc+dyfu+fF0t9rGSjpz8p/aZ4jzzhtTBooE/Y/SkP/C340i8ERwk97332Ee+qgqtsBo1xn+ARyPSx59aVeh0wobfTahU8UUFT2uoCp1esI2eaaujKrSdEh4RAafeFRO8rOlTDi59ysO5TwWs7SsadjEcE9MyfMQo/RPtA1Wh7RRWaDa+4ltODPkWJ4fkwIa+JeAmXvcPzCPKJbGjf6EYj4++qAqtSBFYoR17VUTQhNdlpWXZqXc5hEx8FVv6FYNz77JyX6BYuI37WalZSYMnvoaro/4Hl95l5H5Hsc1r5Oc4O+wrbBTH3BD7+B6/8RlVhVakDKzQa/qU1itrBfiNyygqY3FZkZf3rCzX9wzMJysyY6T5yv2s0A/Gvitft/YrjNCJr8j33xj1MR6MeR+rRSU33qMUWqFIZVSFVqQpVIVWpCnirNCZM2fGjBkzZFYe8tprr8mpEkaOHInhw4fLgabGcKhRo0bJ0cRDhgyRQ6XM4Tbmh1i8eLEcldKpUyd9D9CnTx/5ysEAZPbs2ciXLx/efluLP2jUqBFatGiBN99881kOtwMHDqBv376yzGSFDCVkGgDuHzBgACZPnozNmzfL+QLHjh0rj1OkD+Kt0B9++CGyZNFCIN966y057e+VK1fkSANWzsaNG8t9Bw8efDadGee65lx97733HjJkyCArGSspK33OnDlx7do1mY+C/PLLL/j444/lQExfX185ZvCNN95AxowZZUX99NNP8b///U9+HrcR/kCY04KwYj94oE0j/Pnnn6Nly5bIlCkTatSoId9nPj2EIu2T4iYHA7I5MtvSs6jGNG6Nc/8ldEYqRdrAIhWaGX/iomDBgjL3Q2zQREgIVapU0UuxwyfI999/r68p0hvxVmg+xjmuq1ChQvjhhx9Qs2ZNaYZwO1NVEe5nHgyaBzQFuI+P+3ffZRC8Nv0vEwXSbOC2jh07yu1//vknPDw8pGlTuXJldO7cWb5yaM3QoUPRvn17DB48WB5LTp06JY9lOq1//vlH2u/cRgzTh9dA+5sjjj/6KGnDlxT2S5IV+osvvtBLKUeDBg30UvxwyJMi/ZHoCp2QtFlUcgN6Po4ePaqvPU+1atX0El5IdcAG5l9//aWvPU/FihXx2Wef6WtxY+lh8grbJtYKfevWLfn4f/XVV5E/f37kyJFDeiFOnjyJAgUKSE8E3WmkTp06cHZ2lttoLmTLlg3vvPMOXnrpJfk+ejyY5JBmCd1vzIRJKlWqhDlz5qBdu3aYOXMmPvnkE7kQ2t3MyEP3IN2FrMSE5a+//lqaLvSU0Gam+/DcuXMIDg6Wn8HsnnTt7dy5U76H2xXpgzgVmlk3aR+zEtM1xvzD27dvx507d+R2w7NA+5i+6vDwcLmNlYmVeNeuXTIbJ6chY6VjRWO62Pff1xIH8ry0g93d3aXt7ePj82wqBe7je+/fvy/Py5RThD8qnpcLczfwOEdHR3lNhJ/Na2Mlpl86ofOPKNIGSbahFQpbRFVoRZpCVWhFmuK5Cv008ik8Vj0/KeDRqUdxce1FXN50CafmR2WkDnz4Yvr9iJCEz0UQ9Eh7/4NzD+B3Pe4s6cHewbh3OmpY/PKqet5dwbPsmfrL8empOAGIItV5VqGv772OxeUXYXuXbXJ939C9cn1R2UUIDQzFgVH74VjHEdv/0/Y/ufMEl0Qlv7HvBpZXW47QgFD4XfHFjFzT4XPZRx7jue4iDo07hIOjD2BuoTlY32YdZn4/A3MKzMb0nNpkLDf234D3RW/xeftwauEpLCqzEJv/3oRdfXZiV9+d4hyecO3hKs/56OIj3HW7i3lF52Lrv1twdMoR+WPwvuSNCE5FK9jYboM4xyLcOnQT/jf9cee41li8deQWNv21EZe3Xob7Kj2DuiLN8axCn3fywNOIp7h54AaOCZVjhQj2CcZ55/N4LCrN7aO3pVIbhAWGwVdU4PCgcDw8/1C+nph1Qh5PLm++DB8vH1nZWBkjIyLF+y/gzNIz8jz3z2qTAIaHhCPkcQhuHb6FQKHaVNzzq6NStXuu95Q/GoNLGy/h3IpzODz+EJwaOsltfFqcmHVclu8cuy33u805iQfuD3DB5YLc7rn+Ii6uuSA/66GHFsykSHsk2YZ+Kirok7sJmJskjuHzQd6Wc6mF6wqtSN8kqkJ7bfPCrLwzMSX7ZKmOj84/wsKSC7Cs8lJs7rBJmhtkZ29XLCg5H5OzTpLrZG6BOdg7aI80FciGtuvleVbUXCFNEZohvl6+cp/vVV+p7HwqTBOmyXlnD/kZhNsNFhSfL02QHd23Y16RuVhcbhEC7qtw0fRMoiq05wZPzPxhBlZUX47HNx6zRSYr+OwfZ+Hk7JOi8k2Vx20RlXZe4bnP7GQ2NHncvmH7sKDEfLltWdWlmJJtsjyOdjbtdf9b/nIfcV/pDteers9+JEsqLJavrPhu4rOIw88rcHXnVRwaexDujuewtPIS2RZQpF+SbHIoFLaIqtCKNIWq0Io0harQijSFqtCKNIWq0Io0harQVoCpFPbt0+eBVqQoqkJbkMSMeVRYB1WhLYCXl5dMihMdjtRRpCyqQicTIyVDbEyZMkUvKVICVaGTCAf4JhSmQVOkDKpCm3H8+HHs378f27Ztw7p16+Dg4IAFCxbIlGITJkzAiBEjZJ6+Hj16yFHsTHbz22+/ybx8HKHOfHocKc9R6eXLl5cj1ZntiekavvnmG9SuXVse17BhQzRp0gTNmzeXSSo7dOggz9evXz+Z6HL8+PGYNm0a5s+fL5NQptY0w/aIqtDJgDlHYoI/guiUKlVKLymsiarQyaRp06Z6KWY2bHh+8niFdVEV2gKUKFFCLz2PkVBHkXKoO24hnJy04WCESdgNfv/9d72kSAlUhbYgbMhFx9J5sBVxoyp0ChAY+GLKB4V1UBXaCjAXX3SUPZ0yqLtsBWLLdhpTRT8wcr98DfEPkcl8yDmHc/KVuDu6I9Q/VA5QJkwBcfeklmvEw0kbq8lBxRxMrFAV2irElUP70KFDekmDyXSYzsFIzvPI0xveno9k+gdmsmLyHuY3IZHhkTLXSGR4BHwueWN3311ygPKsPDMxK/cMeUx6R1VoK8CUv7HBFMCWaCgGPQzC4XHP/zgUqkJbBWOaudjo0qWLXlJYGlWhrYCRfD0uniWZVFgUVaGtQExzJsYEp/pQWBZVoa0AZ9pNCEqlLY+q0FaA88koUgdVoa0AJxNNDMZE/Yrkoyq0FeDsXYnlrbfe0kuK5KAqtBXgFHe7+u/CmuYuMmXwjf1RGVEXl9OyqBImgVdYFlWhrYDRG2ikE+YUGuTCmgsyzzXnrbm+77pM/2twZOJheJ7zxKNHj/QtiqSgKrQV4KSgCWFZFS2JO3NmT8wyQZYbNWokXxVJQ1VoK7B582a9FD/X9+jmSAI8eBUqVNBLithQFdoKrFmzRi/FzZoWsR/3wQcf6KUojPnOY4PTS6d3VIW2AotmLpK28sTMmhkRnePTjyMwAXPBzJ49Wy8ljISaOmkZVaGtwKJFi+Rr9ElMk4syOeJHVWgrMGvWLL2UfH744Qe9pEyOhKAqtBWYPHmyXrIMCR2+pUwOVaGtwujRo/WSZcn57bd6SREbqkJbgWGDBsjXsEjg1hNg3x1gyUVgjBvQ+zDQfi/w1x5t6bgP6HcEmHAaWHsVOOsNBEUbehgREYHQkGB0PROGiDCxiPWYUCaHqtBJ4sRDrVJW3wAMOAocuqfv0OnTu7deshxZ85dAd9HG/L5AYfwkPnfsKSD6bNDK5LDDCt35ALDjJlBtvbb++UIgJGbBShbLPYFK64C+Qj2fhOkbE4g1hlhlq1hPpvD9JH9UViZzIp8CPYX619wEuGtjatMlNlmhzTvNci4D3tSdBnvFo7unPi7UQVS46/7AkONAk63atsTCz5lxDqgsfhzOWpYAi8D0uNbA8HLE1kiMyeTYf1f7YW5IJzNG26xC0+78aomwR48BH8zRtq0QlXipsEX9QoDGiazEXo+B5juAXkLFgq2g6OYw57O1iekzEmpDL74ANNoGeMecPsSuSfEKzYpKqI6/bAdyr9AekVPPCHNiP7BNH463UNx0cslPe00Ml8V7Gm4BppzVN6QwLVq00EuWpVy5cnrJsvDHThW/EHv2BbshxSp0HlFxCzgCbwnzgSpbeJW23T9UXMRErfyTuKmJHWZ3O0CYHEJtpiQ+pt5qMEO/NYjesXLw4EG9pGEpL8fNJ+Kz1gJXRUW3N5JdocMjgVLOWtmojNw26iTwm3jEv6In9DFN0xpy9Axk1nqGEw1b9VTxTmIJfDGrls1Qv359vWR9zO1pa7nt9ounar3NiW8cpwZJrtARovK+PBX4YqG2fk2fwaylKzBGVGY25j6e96JLKzFMEyZDI2ErX489s5ZNUqdOHb1kWThviy0wUzSkuz3/cLAZkqXQ54XtS1X+WahuIi2FF1h/DaghznM4GT8AW6FWrVp6KX5CxdOMbkcufLLFRVyxHI6OjvjouwL6WsoRLv7wDUR75eh9fUMqk2I2tDm7b2umxwZRidMCfFptFY1Z9vpV3whk7bEBa65otqgl8RaPfDaa/xUmF+9fV6GS7FksU7IYqg9fgB6iIV2x/0x8/vnn+jtSHj6RG4qnKit6amD1Cr38knbzXW/pG+wUT19hv4sKSxNow9W4XX+cxs0alClTRi+9SLkKlVBz3Ep8kb+UNPv442KDObXpIX50Kdlgt1iFviJaxG12AX+KdsltKyesDxWVqZZQwkbiUTfoqLatwErtNbnsEk+PWpuA/kcAv1B9YyLh3ITWIC6T4+SJE7JRuGVLzMO/+FSsKn6MqSksviHixy7E7aIV3YNJrtC/i8p7xcpTWd8x+2EMFBW3oF5pJ54WP56dwD2xn0p5Tjx22R0+8oS2PyHw5tJb8ptQM/PPsQTxxS1bC8PLUbhwYfkaHwyGYgWz9PdPKMcfiB+Z+HwKlKVIFRs6PtilbXBMfGl2fV8QDdDMukfl1EPgDz0O52oCflT3g7ROnEHHrBP3ER1rdYCULVtWL8VNbDMIxAcrNp9OVPPUYJmn5iVjXEpSSbUKzQpK6Nss6wLkXAq0FQJTdJXWe8jQS9JafEESjwPgGY+FmcAu7uFCrdlYSw3isnWTQ3zKb2k/NO9lfWHW7U4lM4Uht2xgJqbPIcUr9EfzgELCdMi+GHAUDcZP5us7BJ/pZXdhQiSUPsLWpe0ePYY4NTGfpzAliV6h33nnHb1kGW6JRmb5tZqplxqcFE9mdtGzoyc2LFahSzqLLyuUllz0i1Lg++LLb7kOZNMzYL00TVTcBVqv4bqEZZ19Bn+xlcUXYgPUlrHWjFc/5PxOLyUcTq5vLVixaIPbEsm+84yIO3pPs3XPmGWxYiPNRVTY3oeETbkGOJ3IDFe04yoJNdhpR+6+lStXYs0aYYSK28pX89llCfNBh4aG4vr16zh8+LBMSLN8+XIsW7YMS5cule/fsmULjh8/LlOCGSNTGtZvAIy/Boz2xKAqsYemFv+2oF56Hp7XfLCttWCs+hzLDnRPNBaRko+01G34MokxGqdEZWdjZMF5fYMdwQaYs7MzGjdujOrVq+Pbb/MIg9+EHN9YtgI96H8YLQrWxr9fdMSkzBMxOdsk+To91zRkfj0zfDl0ZvRFeHXdhlOnTunvArp16yafGFxSMsE67W+aB9Z24UYnxW1o9iTVFpXXCA+1B65du4a+ffuiatWqcHFxiXG+QYNvc7whX3PltGzOZ2PmrOiVkutnl5/Fmc7rMKB8e9R+rzYmZZmIiaKyLyqzEMenHcfJ426yQhf55kccP3kiVWa2ZQcbO3usjdUqNFumHPhZRdjKB+7qG60I7XHDn2manLTIsAsXLqBly5Zo164dbt4UNlMScDt1RvwALPvcPXvmHHIW+Uhfixt+B4Nw0VL22nIZq+s5427f/cCYy6jxc40ETWpkbdjjusMK5qRFKvTkM1ojj35Ea2O48z4UZs4Nf2CFaCiSN2Zq4wB5HUYEYJnV2mt0qLBz5syRirtvn+Vko3y5jNLcACzb5zxJ/Jl6ucf9p/o+9zuiosasHFTkbj2E6fH6qxg/fry+FQgKCpIjX0aNGqVvSR3YyGcHC70oySXFTY6kUF1UUnpGXp8BLBECNFkoP6ESk0/FPtMUIGO0hEVeT7TKO3z4cDRr1gxXr17V91ie8FBxK8N5Oy17S9tuNmF8mAkTIuI+b/tSYv/UuI/5rFBh/OMfICtybLCRynuV1M4ZS8BAr/pCwZMSemDZu29BpJtPNxcrrdGKdA2+MV3bls8BmBjV9nkGk7w0b948ySZDUilTJhNuXxe3M56Kl1hmI59U6Kqisl6+HnvDw3u4+NzJYpkS++d/V+UndBFPuK6i3EKYVglh3bp1aNKkSay5QFICRmUyRPVRAn5jlr378XA3WluErjz6pcl6IZ4But3r5acNGDDaP12E+RcTvNk///yznAIi1XlqEj+i4ggL26NvsAynT52VFTo+mhY14fEoExrP/RLBETHHrTZr3x7N9h9ER/8n2JfECjpmzBj06NFDX0sdOPaxxkZgTwxd9Fat0E6X9YKAPuXHosL+bfb3Zp89/dWE0W1V12npCWLizOnTMnCePlVbY+E8E4oXs86tzFP4G1QfnLBz5/rBhM40PWJhb1gYAsXym8dFFC5RQt+aPH7//XesXSv+uDaCRf4KHGVtQMOelZPd0bRxzc0CRsbRE5FpntZ7GJuNdPfuXWnHjRw5Ut9iuwwYMET8y9tonYiexvNNyPWT5gqMjwX3mgIz4v+T9hZtiW562ZJwBl2Gzj5+nHpducmu0FuEAR8olNcwHzgYlvyxE2i5QyvHBb/8H3/8IbMNxdVYsV1MoiFlvXkGJwpTxsktYckf6auOFDb0gUNCUeLhu+YtkPOX5vqadZg4cSL69++vr6UMya7QH8/XOkmqiKfOXiFScQUJ8RfMBlvPnj1TxblvaerWMaFHN4s85GKF9vNTJDzyqvz3JtTKk0Ffi51jwvSgSt9OocYzvSZs75w8eVLfYh2s9teg+4e52FavjsUZbOe4uXFckQkhIbrT2wqMHjEO/a8m7k806ETxOD0d5nxUvDhanDmnr6UsR44cQe3atePsdU0KFqnQDGifMWOGxS/Olgl6YkLDhtZV5yyioZmjauI+IzRMNEymmXDjZvzdcEEhIfgvNAz//fuvviX1GDZsGAYNGqSvJR3r/kXSKHnyZMfRQwz20TdYiQHXTWg6uJC+lnDaFjWh2Lfv6WtxU3XFCqs0EJNLq1atkjS1h6rQiSQkRCigaKgFBDTQt1gP2s9ePsf1tYTzi+P/EDwu4X/aaouWIMuP+fU124QxNuPGjdPXYkdV6ESTF8WEAlqbp5FPkbt20j4nEHel2ZHQ7usVoaFSpe3JZJw+fTp++eWXF1yEqkLbMskwaWbWN6GwMI0Syh9iuZ8G2kDpokLny/MDutfNlSrLcb1bfuCAAVZfRplNVlS+1/tafEc0OlT/OsbrtORSt8gn+qelPOmiQpcoUhAre1VAsN+rCPV/BZcOfI6A+2/CsUdFhIht/vfehNuaHPKYO+c+wkOv97B2aCmsHlAWvjfexrphpeS+B5ffF2cz4drxT/FEvN/r4Odw7FkRWycVwcqe4vy+r+HYyu9wYeeXMoyU7zl+QvO7OvepKNe5/HjuQ/maUVzLRw/fwA8X3sdHD95A0VOfIKPfK8hyM6Pc//WVd+AkrnF194oocupjfHv5XTj2Lo9M4tjc5z/A2+LYrNfffnbevF9FVaTrQcL2FmZHdBZ00r4L9xQ9swfDp7aT6/3ndEG7VWOQISxcfF5pOPSuiJ/3rsT8wbXl/lq7V8C5R1kMnd4BL0U8la+repTD3KH1sFIcW/Hw+mfH9m2UW/uwVCDdVGhHUeFWicoQ5PM6PPdlFltNWN2/LBy6V8Lh5d/juHNO+ce4KSrV/Uvv4YFYWKEdRIUKD8yAux6ZZOUND8ggfwiPb78Fl4FlcPXop3h85y3sX5RH7uc5GHHnMri0LMdUoXOKc/PVFG5C/rOZkP3a2/jyllaJXwoxYXnf8hg5pTA+E59R8vj/MHlsMcwfVEZsLycqVUW86Z/h2bHGObmYV2ji+rcJP9eup69pmFfod574Yfi0v/DfkoGyEnNbhrAIvWKWR92dS+HcvQyy3L2KV0LDUOb4Vrzn54OC5w5gdbfSmDCuFWYNbyAqdV1U3b/62XWoCm1lDIU+s+lreB3+HKfWfy0qZQUccfheVOCPsWt2frmfakyl9ToklFdUHOd+ZfHIS6iiXlG5PLj4vqbKE4vgtlDzc9uyYYX4UTj1KS8r/d75+eSPw23dN/K4mCr0a4EvI9Oj1/Fy2EvIJBQ6+7V3nu3LEPSSfGXFnSQqcjfxQ/n81lv4QixU7mkjS4j3vI5V4jqNY40leoX+tl4GWanNMSr0zBGNxDnKix9JFbnOSkwFnjW8IVbp51s08Odn5144qKZcnzOsvjyO69zO4439xrGqQlsZxvNWKFEgVRavK1quBvMKba0leoV2j1jzgtnBCu3co4wwZcqJilseTj3Fq6jYfD9ftaXcs3NG7ePToawsO4lXlo3j5X5xLh7DRVXodMCaXpUwcGZ+uHSrhMXC1MlyIyPef/SaUL0yQh1LY46w2WcLW721i2bL577wgXx9KfglVN2bGePGF8XU0cWRTdjMNFVeEerMc/H9VfZ/IZSy5AsVmtwZZEL3Xn30Na1Cf3PdQ1bo4m47YXr6FP97eBvL+v6ED30fyu3dF/aRyru2awlZQXgd319yk5Wfyu4izI2cV86K85xHnZ3L0GzzbLRcP02YRbWkKaIqdDqACr1Q2MGDZuTHu96vove8vPjL8TuYhL1tErYwG39OwkRhhZ4jKnZe0ehjRWLF7T0vHwqdziTXTaHi+DATMoiK/o7vq1gifhy1XL+U+2Kq0NkKmTC9ftSfmRWaNu97ft6ocmAN1nQrhb9XjpQVIevty8KWLiPMnL6yQrNsXqFpT7OxSPPi5YhIfH39AmrvWiFNlJbrp2IezRZxjKrQ6YDVokLPG1Ja/vGX9+Pjno9p8VjvrS3G+rL+2j4qL1/n6+/hwvez0nObsZ3vXTJAe09MFXpPyMjnzI6RLfNjyp9FxFI02mK+LaZybNte3P9X1a/1T0t5VIVOB4SON2HpCn3asTSOqtDpgDxfmfB3yfTxp1YVOh0w++Kv8aY4SCuoCp0OiBQNuN+KmRASHKJvSbuoCq1IU6gKrUhTqAptp/xaITuceleMd3HpU+658tq+ZbGyd6Xnjoltof/Z3lAV2k5pUT67rHDxLUwPtmNAQazvWxLuw7PhxuiPcWBQnhiPjb449LSNqZgTg6rQdkpCK/SZoV/De+w7eDj2PVmhb43OhLCJr8R4bPRFVWhFipHQCp2cRVVoRYrBCn1r9Ee4OvJTocJf4fLIz2X3t2OvinAbmgOBE15H8MTXcGBgHjj1Ki8VmpV0e/9CCJjwhjiuAvzGZ8SVkZ9h74B82NqviNz2YMz74r1vyGVFD2VDK1IIVmiP4VmxX9jD/uPfxOURn+Pu2A+wpm9pXBiuBSvdGv2JUNmKCJ7wGp5O1mKnXQcUwL0xH4hGXzmxrxJ29i+AfQPzYlu/wgiZ+Cr8xmWU7+EPQym0IsVghaYt7DEsqxxIwAp4bmh22Qhc3rMy9gz8EbdFA5CVkwrtP/6tZxWaSswyK/D1UZ9gv1BxVmiew3vsu6pCK1KeLl26onv37lZdunazxRQ0caMqtCJNoSq0QqFQ2CjJEuimTZsiLCz2+QDPn9dmhl2yZImcBdhg48aNMllpXDCNmZubm76WMJjwf//+WOZjiQN+hxUrVsjy5cuXUbZsWZQoUUJODksmTJggE6zu3LlTrtesWVO+Ek42MGQIk/hDzo7GKQB37NiBMmXKyDk6DZg9lgk2Y8Lb2xufffaZnJCW43mj06FDB5w7lzpZbxUKReqRLIHOnDmzFLe3334bDx48QMaMGfU9muh9+OGH8PX1lRMTUOTWr18vp3mkGDJRarFixTB16lQ5nbvB559/Dnd3dzkVzenTp/HSSy/h3r17ch8FrFSpUnL7V199haNHj+L999/Hrl27MHv2bNkuP3ToEPLnzy8fDpwr4ODBg/jggw9w9uxZZMmSRZ7HHE4szHNx+ngKKh8KH3/8MYoXL46QkBB5rocPH8pj+QBg+nZ+X4MrV648E/Jff/0VXl5e8rO+++675x5C27ZtkwJdo0YNOWvikydR81RxMo69e/fKe8gU8ZznoEGDBnKWbs7vRdH29PSU95MPBE5Dz+9XsmRJrFmzJkZRVygU9k+yBHrr1q1S4GgRky1btshXA1p9tJwpYhQWTqpy/PhxKbic0pUiw/nAzAWaokghp6AxTyrLhILPSQkpXsZk1pcuXZKvxqQdPJ+Pj4+0dDl7DkWNDwg+DBwcHOTs7SRHjhzylWzatOnZjJJ83/3796VQU4hdXV3ldoo2PzsgQJu4l9fM/cZcG/x+FMpbt7SU+ceOHZPXze9iQCuZ100B57HmE8zwuv38/OS95P3iK1sQhlVPkaagG/eZDyFeM+c4njdvHj799FO5XaFQpC1syge9Z88ei8wvTUvUXBwTypkznATIcphbybFBcY4PthgUCkX6I9kCTfGgq4KuBlqJpUuXlpbrP//8Iy0/+mc7deqEIkWKSFcA/bS0Rg8cOID//vtPnoNW7ptvvomqVatKy/PVV1+Vx86fPx/Zs2fHe++9Jy1wuh4KFCiADBkySNfDF198Id9PNmzYgNdff11Ow8Em/zfffIO33noLFy9elC6WfPnyST8vr43QOucx5H//+5+0VuleoZXMV34nnqt69eq4ffs2fvzxR3ksP/PRo0fyXPxO7du3x8CBA/Huu+8+N/31n3/+KR84kyZNwuLFi6XVTKu4Xr160r/NzyT8brSYaQXzu1WrVg3Xrl2T2+kmoRuHlj+t9Jdfflm6QCpXrizv9YABA7B9+3Z5HoVCkfZItkBTfCmuFDAPDw/pf6WwUujokyV0KVD06EMl9MXWr19flg1y584tm/10GyxYsEBuo8uEokth5vn4ECDvvPOOfKWQm/Pll19KAa1Tpw5u3rwpfdZz5syR53vttdfkdZpDN0HRokX1NeCjjz6SFjx966+88op8kJCCBQvKVwo23TEUdwoqHxR0i/Tq1Ut2AppDUXZycpJlirPRSUofPM/NBwbhdRF+BrdT5NnRyO9KQeaDiWJN2FHJbYS+eLo3FApF2sWmXBwKhUKhiCJJAk2r1N/fXzb1aZ3SouzZs6fsPCPsHOzatau0Lr///nu0aNFCWsAMgWNkgtHRN2XKFGl9GtDqHD16NMaOHSs7+djhx/OyI4+fR+uS2ydPniwjNtg5uHv3buleoCuBURZ0K9DdsWjRIule4fH8LH4uozoMFi5cKI9hlMfSpUvRv39/OeFks2bNpAuBvmHje5j7ptmBSEub1isjLdga4DUTfse+ffs+69wzYOchvyfdGuwk5HcivN4RI0bIMl0vvMbffvtNWtCMeuH3ZYcgr4HXw/Pz3vO7s3XAcxo++0yZMslXhUKRdkiyBU0R44y0hL5eRjow8oL+ZAoRQ+UYzUBfLOOg6f6gC4I+ax7PCBCG2JlTt25dKcYUOQofw+NOnTqFXLlyST8ww+EoonR5ECPcjYJJFwOXoUOHSkHj9XCdE/vXqlULjRo1kuF4BkZIG0PheC2MKuE86XRrGP5zCj+/B10j9BOToKAg6QLhuelP5sOGbpm5c+fK66Ggmkez8H10S/B70/1CtwpdFgyro3+bIszvS5cPr5Ex1Lx2w59NNwqvia4ePgjpZqGPmtfKKBa+ErpEjGtUKBRpA5tycTAUjpaypaFoskONr7bK4cOH5TXSok8sRrihQqFIWygftEKhUNgoSqAVCoXCRlECrVAoFDZKrAI9t9AcHJ1yVJa3d9mGRx5aPgoSERqBGd9Nx123u3J9UdlFiIx4ipNzTmJXv13YP2IfHpy5j5X1VmJ1Ey0WeFGZhfKVXN15FTcP3oTfdT/cPnob7qvcgadA4P0AnFtxFsG+wVhRbTmOTDwsP+v86vNi+zkEPgjE3eN35Dkurr0Iv2t+uHngBs47echXbpOIc513Po9bh7Sh15c2eMr1B+4PECA+Y3LWSfAQ7zG4sf8GTi1wg9fWy7h74g7uiIXbnp1PcMHlgtwWnSvbvHB582VZXt3IGSdmHpdlgxv7rsNzvSdCn4TinIOW8OjanmvwXHcRV3ZcwcJSC3B50yVc33sdkWGRmJlnBk4vjBo5eO/UPWzvuk1+//DgMDyNfAqPle64qV/L7SO3cWHNefmdDa7tvia/L4+9deimdg3iHigUCvsiRoGeX3weNv29CS7NV8NdCAMFmoJAcQsPCsf0XNOwqd1GLK20BL5XfKVA+9/0x5aOW6S47B+uCbRjbUeEBYbh2NRjWFx+kX52yPNs+GM9Lm3UhDPwYSDWt16HxzceS1Fc08JFnGuzEMTrCPELlp9DfK/6Yp047qF4WCwsvQAXhchxOe9yXorchTUXpMjOyjcTD849wL3TWpKl2T/Okq+OtRzk65SvJsPvqp8skxv7hEDPd4Ovly92dN+BvUP2wueyD+6fvY/j049jftF5uOd2T4olofAxYsK15w5cWHtBfAcPUXbFzp475X0wjiG8VocaK+B/2x/zi82TIjw73yysa6WFJC4oNl++Hhp3EA88HmBxuUXwueQtp3sl/MyDow/I9fkl5mP/sH3YN3gvnBqtwqMLj+RDZ22rNbh9/LY8PuBeABaI4/iwXN1sNbZ22iLvGx+KpxedkscoFAr7QLk4UpiIsAj5ANjWeStCHqf9ubYtBVMIKBTpjRQV6J19dsJjlQciQsKxuOxCaV3GRqh/KA6NjTssbnm1Zbi666q+Btw/cw/OjZ2k+4UW7u4Bu+BUfxXW/rrmOReAwbwic/E0IoYdycCp4Sq9pEE30Rrx+ZOyTMTDC7F/X3NoGT88n7Bj0wvMjaJQpDesKtALSmrN97sn7+LgmIOyqc+m+uObj6XbhLD5vrqJM666XsXy6svg2n0HNrbbiCd3nmBnXy1BvgFdF4TuhEcXH0lXS3QiwyOlSNK/bQzcWCVEmu4TQkFeWlFzmSwsuUD6wJdUWCw/l24XuliW/bRUuiGCvIPkcebQBbGq7ko4i2teVmWpFP4Zuabre4G5BefopSjmFJitl6LY9Ncmea4FpbS8I/Qz8zrJOcdzuLTpEi5vugyHWg7yXqR3jHwoCkV6Qrk4okGLnL7bpZWX4vYxrUNSkfrkzZtXLykU6Qcl0Aq7wMj+p1CkJ5RAK+wC5v9WKNIbSqAVdgEnR1Ao0htKoBV2AWehUSjSG0qgFXZB2bJl9ZJCkX5QAq2wC5i7m3ASCIUivaAEWmHT3Lt3Tw5SKV68uL4FaN26tZwYQqFI6yiBVtgcnE6MImxOzZo19VIUhQoV0ksKRdpECbQi1eG8kZyJff369fqWF+H0YjHBKdFmztRGmCoUaQ0l0IpUgcLKjr+ETnHG+RrjomHDhnK+SIUiLaEEWhEjoaGhePjwIby9vaW/lxPWPnnyBIGBgVIIuT8sLExOgpvYyWo54XBi4czwCaFMmTJ6SaGwf5RAK1IFir0xK3xC+OOPP2AymRAcHKxviR3OmM6Z1q0JH0p0zXDhQ4qzzSf2QaVQxIcSaEWqMm3aNLi5uelrsdOmTRv5+tNPP2Hw4MGyHJ22bdti9uwXMwcqFPaKEmiFTVC4cGG9FDN//fWXXoriwYMHKFmyJK5du6ZvUSjSFkqgFTaDj49PjEJMOnbsKF8XLVqEVq1ayXKPHj2QJUsWWVYo0iJKoBU2B10Y169f19e0CA7zgSrRyZAhA/bt26evKRRpByXQCpvFzy9qYt++ffvqJYUi/aAEWmEXDB06VEZMxEemTJkwYMAAfU2hsG+UQCvsgrFjx8rY64Tg4eEhQ/IYyhcfPl4+cv5Hg/3D9sn5LpPKrcO3MCnrRESGR+hbouB8mCtqLNfXolhedZle0gi4G6CXFOkdJdAKu2Dq1KlykIyloaAeGLlfX+OExDvgc9kHi8oshO81X6xu6gy/676Y/u00XN5yGQtLLZACvq3zVlzZ7iVnkA+4+wQuv7jI2djnFpqD8JBwuDuek8fcO3UPjrUc5MTJ4cHhcq7LPQN3w3ODJ9a2XCtntp/27VSEPA7BlGyT8TTyqXYOcaxCoQRaYRfMnTv3OZ90QuFQclrTnp6e+pbnCbgfgNMLT+HUfDd4bfXC7aO3pFhecDkv9985fkeuB/sE48ziM7i+5/mQvojQCJxdehYP3B/IdY9VHvLVQNt/BndO3MFT8R9njQ/xC8axqUex5Z/NcJt3Eu4r3eWx7g7n5Ovdk3fEebRtivSNEmiFXbB06VI57Dyp/Pfff/j666/1NYXCPlACrbALnJ2dZW5ohSI9oQRaYRds2LABt27d0teSx5YtW2TstEJh6yiBVtgFrq6uFh/SnTlzZvTv319fUyhsDyXQCrtg//79uHz5sr6mUKQPlEAr7IITJ07gwoUL+prl6dChA2rUqKGvKRS2gRJohV3g7u6Oc+e0MDRrwYkJGJJ38eJFfYtCkboogVbYBV5eXs/ljQ58GDVoJeBegFxC/EL0Lc9z8+BNvaRQ2BdKoBV2we3bt3H06FF9DZhfdB489AEeU7+egnmF5uLUglNynQQ9CsSsvLOwvs16LPtpGc6vPo/VTZzh3MgJ513Oy9F6m9tvwrwic/V3vEi1CtXinMhWobA2SqAVdgHnRzRSiq5uuloI7NxnI+8cajlIwb15KMpS5gi+ZVWWYmHphXCs7QBfL18sKDEf8wrPRVhwOJwarMIisW9JpSXy+Hun72FFteWYlHkipmSfjK0dt8jty5cvx5tvvinLCkVKowRaYRcwmf/27dv1NctDAd/Vdyc2tduInT1d9a1RcM7BxLJkiSb+CkVSUQKtsAvYgWcNd8PJOSdxeXPCw/f+/PPPBCdtqlixol5KPDdu3JCT3yrSN0qgFXbB48eP4eTkpK9pBHkH4eSsE/pawmFWuvW/J13sK1WqJCevjY8RI0bopcRz9epV7N69W19TpFeUQCvsAuZ2XrZ8GR5ff4w1zV0wKctEmZ5z9o+zZOfgnkF7sOmvjVjTwgVrW67BulZrsebXNbKT8NC4Q7h/5r5+JssQEhIS79DzdevW6aXEw8kJwsLC9LXE8/vvv+slhT2jBFphF9CtMG/ePH3Ntohu2Rskx8VB8T948KC+lnjq1q2rlxT2jBJohV0QHByMadOm6Wu2x6uvvvqCj7xTp056KfEk18WhhsWnDZRAK+wCTnc1btw4fc022bp163ODaQ4dOqSXEg/dGwEBSZ/6qlu3bnpJYc8ogVbYBQxzGz58uL5m++zauRPZKtaVln9SuHPnDo4fP66vJR7l4kgbKIFW2AScr/uh0LLzvsC6a8Cok0C7PcAv24Ham4AaG4EfJ5xG5/3AsBPAXA9x3FXg8D3A0w+4JYxN7xAg+MW5WpNMiDiXjzgnz83P4Ge5XAFmnAP6HwH+FtfXeBtQbYMQxA0hMGXOjyLt+qP+nG1os+E8epwHmi07gAZzd+C7ms3RqH49/czxk1wXx8mT4gYq7B4l0ClM5FPgXrQwWk8hSh/EPuLYLggIB848AmYJ8fpT6ErdzUD9LcA/+4CZ7pq4Rf/eiaV79+56ybbJVrgcurpHoGyX0ejtBeQrUkzfE4VfKHDsPjDlDPDHLu0B1HIHMNoNOHhXPKz8QxHon/g5GA0GDhyolxT2jBJoC/BEj4Y69RDIuwJ4fw5wVohVv8NAx72aBRYhhHn7DeDLhUB7YXmN1dNG9BHHbLkurENHoMlWbVtqEyrM2TPewFQhHi1dgZrCgqXQrrwMXHmsfZfUIDmdbikFIzpCdLeGEcVx6+bNRGfi4/RebtGsYNYj/g3YsqgurHYK+2rxAGDLIzrKxZE2UAKdCMYLUa28Viu/J0S45yFNdBsLYZ0tfn+thAVEBh3VRNpb/+FQuF+ZBlwT4maaKn5QQcDP4ge21CyrZaCwQLeJc1kLXgsfBF0OiCb5eqD1TmCZJ3DziX6AHdCuXTu9ZB+0bt1aL2mw4+6rr77S1+ImOS6OAGEwrN62D/8e1NwvncXf/ICwytl6U9gXSqDNYP1dpUcn/egAfL8c+HbZ8xWb1rJJiG2OpcLSjBDlScC6K9o++iW575P5QNbFwCXRQvUSonxcNGWt9eO46Ks1k+tsBhpuASaf1azctPhjbNWqlV6yDzw9xRMwBhiSx6HrccHOxeTMYj5q1Ci9FDNhopXEesmWUeV1ou4Ko8LDR9+psBnSvEBTPKuICphTCG2tjZoIVxRW8I6bwH1hyb40Xdv2xkxhaYjKukYcv/OWEOAlQJCwaml5hMcgdvQhWhP+WOgG+UlYu+yImuMOXPfXrjW90rRpU71kHyRnoMqDBw9w6lRU+tTEYgkXB1tXY9y0OthR/DZOPNB3KFIMmxZo9pxXj5YygT3rR+8J8RIVhz38783VXArm0P/7/QphqQhr9k4AkHGWJrIPhCB/LYSXwvzObFEWVvA/ZvloHsXgy7M0FHY+BNgh9LN4YIw4AbgLQym1/Lr2RIMGDfSSfVC/fn29FDuxTVyb3CiOTZs26SXrwc7t3oeBCsLgmSCeJTH5whXJI8UF+qkQoq9E8/9/8zURJeVdgHNCVK8JC/FtIabmfDwPKLMamKn3sfQ8CEwTzfhgYd1+qEc+fCrOdVsIsQF9ufVE/aTwXRXnTAmor+fE5w05plnsv+3UhNjXypZ2esLeOr6YwzoheHh4yKm2zOEglbt3RfMticyeLSyQVIQulA3XtNYfXW/bRYtV2SCJJ9Us6N6HhPgKYV1yUSuz84oUcwJOm9XrQ6KOGh1zM4Qwc1Yj/xQWPXbgsUOtgaho7D0fcxI4r/x1KU6tWrX0kn2QHBcH818ztWlSsfWH2QVhfXfaL6zvNcCiC5rhpniRVBFohgtlmKZ1xKV2s2jPbcjBD2VFRWknWpT0TStsk1o1quklzUK77KdZZnPdtU4uxl/XES0ndnpVWa/5TquKB2o98WD9fRfQVbS+hh3XonGmixbZAiEMDpdES+eqNujFWNYLy4+LsxewXDyY55/XQg5HiwdzL2FM/LUHaLRVOzc/gy2mSsKI4AOcnW7DTwCO4r2Fy1ROdF+Fv/9jaU137/IfOp8MQvkKFfQ9iYMzwdgrvGdDxd+ppGg5c8CSEcaaHrFpH3RS4Y/XVfxwuwqrnD8e/jj5wwuz4CgzReKhn51uLP4thggRo8gx5I++ePoyGUHDyJfYqF49SqDtAaZITQi+olXoeguYIFqIzZeex5f5S6DruTB09wB6iBbmtz81wIY1LvrRCcPR0VEvpS0YnbRQPFjZ0f+veBim9Zas3Qh0uBDds97C8hGVWFov4oc9QjxdTz2y7w42fp/BwvozD4tjBfxB98/bKrRqdovWx6BjmoXKv8e/oiVCi5QibI2/SUKS5NsSSXFxMM/0F0UrIU/+gjjl5obmvzRH7sbtcfasMOHN4O+BURWj3MSDSzzgGGZJq3PfHS36qF699DlQhRFYbMkwgIBlew83TTWB5g/4ujAw1gtriv7nWqJp2lAIL/McMMSMFdAe4XXf1Yc0zxcWEDsyM87UhkJnXSR+VPe1gQSEQ6Nfmw68OkNztZCSzprfne9jcz2lYKuDnap8YDTZpjXd+x3RXD6PbaSjkzOZ2BPVq1fXS4nHPIpj6dKlyJgxI54mwlFrnpr1sahva8XvrA2HlG/QWiuH7mkRUekJ5nn5TxgRvAez3VMmaiu5pEkXR0pBAaXVwt8NB6xwVGFTIW4brwO/uYofiW708Dj63I2nudtD7XhGonBkIf1srwkRN68w9MNdfayvJAOGFvJ6ft8pBG4d0P2g1py2FdFNDBWS6I9NLRI6d2FMsJMwek7nzz77DEOGDNHX4iaxE+yyah4WxgP7Y+i/58PZXRhK6SX8k0m2VorWH1uCfJDRSGLKg9RGCXQ0KKKGBcx4aj5xGS6U3xFYeB54N1r0EkPrTFO0SBQpvJOjQuuYZ+N1IbwcWVhxjRYN4uUH3DQLCUwqjO92FBWqxQ6tUg08ChwRPzBawmmVsmXL6iX7IDlRHPRf37yZ9B5ra0Rx0IBYIH4DTOzUSjzw2epLL1Y4gxnmiBaxkQOFyb9SQsDTnUAznppx09kWa/kyGLL30TzgvhDlG0+EAIttNBoyiW2Z5mr+PD5ZObSb4UAFVmrniY6lLI1A0RzdJSo+IwVYGZjvY/8dy6bRtFdKlSqll+yD5Lhk4huownPXqFFDX3uR5ExYm1Qo4HQdsN6236u58NILNL42CkOOOW7YH8D0C+ZjM5KKXQk0XQH84gbURFYK5sBg0yzXcs1VsMZL229AVwPzarw6XfMR08qlpcle4AHivcyX8b8FwJeLgLV6Xg1rwAiFcae0NJzsxKDg0xJWxA2nkvr0009lDouPP/4YGzcKE87GafFrC5w583zHXmJ49OgRLlwQFSQO/P39ZUiel1e0Ci84cEAfWGBDnBaCzf4mRu1MOq2539ITtMIZqcTOy4RiEwJN0XyD4qlbofXFE4ii+694ChvuBkJfbwZxHN0G7NAiTGbEnAF7hdXJpj6hAJvDji6ej9YwF0vDMCkKO8P5WPno2jj+QFjVadjdkNJ06dIDkyaY0LFjZ32LbTFy5Ej069cPPfv0QuNmTfCw/yGMrtYVXXt2R68+vdGnTx+4urrqR8fPxYsXsWCBsBqSAHN42NuoS3/RcuQkDPz9cACLGgimYTMWNP27v8bQr2GaqBd0hh7TXA6EIUXWDqM5+VAbBMGeX3YesDecgqywPitXrkTjhhkQGmDC0zBRVcO1JSLEhIb1TcKq/gwtWrRAzZo18fPPP8tkSm3btsV///0ns7ktXrxYWtucG5DW6PXr12WeZWaJ8/Pzk514DGuLjIyMceE0W9zPYdfMPscERvQLX7p0CceOHcOWLVtkhMXo0aPRuXNnOfKvVJnSWPvrNGCMqKRjPFH2qyKYmG0CpueYhvlF52FD2w04OfsEbh++hRA/YVLp3L13F+7u7jh99gxOuJ3EfyVbwrXNAmzaulluOyf2xZYdj7mmP/jgA2lNG8vQoUP1vfYPDZ3N17Vh4+xz2Z0IC9TesSkXR19heVpZb59B4WXeDPrLmos/+mLRmryXzppcKQUnQGW+CYpZ165dZdKjqlWrynzJFNJdu3bh9u3bcmLYmChe/B1cumBC/h/fh/sZE6r+9Kq+x/agODqsjBok0qF9e2TJmkWWI4Ij4H/bHxfXXoBrjx1Y9tNSTPlqMiZ+MQGTs07C9OxT0f6TDmhXrDEwWojxqAtw+GU8WhdojUvrPPHw/APxsIr5HrFTMXfu3M8E+p8SzTFhcjTrJo3C8RFtd2vWt+NlrUWeVrApgU4uzFLH4bnsZS2/Vvw49mohZT52GFIWExxuTFokLoLKokREREjf6pQpU9C4cWM5eKRDhw7S2r127Zq0OC2J+czWtGoNEjpKL6UZPGgIfv/9+UT9iaFAgQIoXbAEHjx6KO5lKGpWq4GPMn6I03NOYdNfG7GkwiJMzzUN4/83DhMzC2H/chKmZJuMtp/8gZJf5odP/8PwH3xCinv4CHf4DzyBMVW6Sp84WwTpjTuB4m9yHCi3RuvDsje/t00LNCMjmNJwljvQTIgSfcycHYLxxpyVxJ4xXDP0vbFz88M5Wmwyp8nqcVBY9OeBWsK6Jzw21zKto5N5TEgV8QAyBDu5MOvaunXr0F5Ye+XLl5duAhcXF9mcT8zgCGvQtOkvcN1mwuCBJmFhi5tio/DB9cPPGTDpqQkVepmEGCY97IbuEnfR4kgK5cuURaSwvqvnLINT/7qgW8nf5HaKM1sxnBmd0R/NmjXDqlWrpKsnvcLfHmc1YroBGnO0xG0NmxHo1JUBy8AZoDddixpwwg5Mfi9OAsqsXUyDWtgsTI+RJAzv+3SBFuo3Shg+3PbmTC2+9AchyOz8ZF4RTrhKcf5OnJOwR5wTEMQGrU36XceOHYtq1aqhSZMmmD9/Pq5csWKYioX477/uWL5EVE0hdtLvLKppmdK2a0u0/aMdhj8yYXyYtkwW19u4cRN9b+Ip8534rtNNqJnnFQQGJtwSoU+dkR0GWYUQN9iyFT+Lv39CoX+dPnXWGfrUd+7cKV1U6RGOa2C+eObzYcKs1EjaZLu13s5gDopuemQTc4UwaxrjqOtt1oR2sXhSc3QgB7UY1j99ZszExuHdnPEl9wpN0OlDYwxpTMYrLdrz58+j76ChMhaWHWOLFi3CrVv233MSFhYML6+XUb6cCdev6OKsC3S9eh9qB9kYeUpnwXdVTfh5uAkTIjWBniheq4n1pLh7Tl8+hI1txXeerC9TTcj3zSf63sTxZalS6CZeu4j6xNc8f/6F7Vu3yX1Jhd+JE+OyH6FevXqypZUeBZyt2q3C4GK4LAfu0PdtjYErrP3pHsY/M7k+4VOSsYochk0403Z5Yf0yzpojC5mvmhZtQWEJM4bagFbzy1HpD2S+W87oTZg8iANQ4iMoKAgLFy5E7dq1pW93woQJdmHxWpIdO3bj0H5NlPPm5WsGdOtmwoYN7eV+WyQi7CnK9zBhkrjmz4uZcBWu2BbWC1cendaPSDjNOzUApojvPU0sQqCDxpnQs6IJeX4wyciRxFBKCGgP8UqB5tI5LAL527dHrrZt8SSWDtnkQrGeN2+eHEX5+++/4/TpxN+DtAKjzNgfxglHOHMS+8gSS5oUaMYhFxdWKfM7EworhZdPPboSOOrHNEGbAICuBIrwFvE0JPkctOgOuicu+Gizd6/w1JI68ZW5hOmSqL1JmzwgOoyHpm/LHFq9HDjAWZ1p9dLHm9hcCemBRg2b42mECYH+JvzT4WXxY7cP/2jfXv0xTljOPc+aMMX1b31rEhAiOgJvYQVqY+6TKphUSxPqovm+1Q9IHH1mzMDnlSqj8bVryFrlJ2lFF+nb7zk3SEpDFwp/B+zrGDNmTLyT56ZlOOn0SmEMMkkck5MxlDA6diXQ9PGWFU8jxkXuEi36ci6aUNbcoLkFzGGsNK1dDulmdjxavIRPM/qEOUsLXwlvVDOzlh/XE8qNGzcwffp0OTCAli+nGrpzRzw6FYmiQIH3xb8mrHUxwe3UF9pGOyFf3QzSev6isAkRsEzvNR/qVYa/jZDxJtwfaoKzyzp9T9LwCAlBpvwFpEg3cN2FI4eFFWNj0Prm4By2HhnLTldeeifVBZqpNvM5ajknODqQ1i1nUmCCoVVCZI1kRIaDPssi4IE+uvCtmZqYcrTh59EGXf0k6jMXTjybFNi7zYEIDCFjh0mvXr1w5MgR2VuvsBy+vn7o0U1Uw6cm8YATAheRDAs0FXBxXofB90wYLaz+NhNK6Fstw53I48iXS9ybqSa0Lpr8n+oTUXez1KqFLuER+PvhI0wYM1bfY/uw05u/RxpCLVu2xL59+1I9wiglSHWBppuBnWNM/s4IBiYvYhQDYeY4Ri98vjAqvIwwfSYTGyUFNqk45NYQ3o4dO8r15KSGVCQNBwdnXHRnFTShsLA+w8JiTw5kq2TNm1Faz0Vam/DwqeUtvgmeVbGFnYbTTbK+WoISw4fj7weP0FXoW706dfSt9s2JEyfQqlUr1BHfh7lb2J+TFkh1gSa5l2udcHRbJCWUJTg4WA53nTx5Mho2bCiH/Y4bN052UKTXECFbp1o1JrM34dF9E/oPyCAsZ/t7QHq4X0SHPSZMiDChTCtttKCliYgIw3dNXhKWjAn7Oppw/sJFfU/yaL1rFxrv2oPuopyrQEFtYxqFA6gGDhwoH3DseOdwf3vBJgQ6OmzOMGxs8+bN6NSpk/TtNm/eXPp3KcSxDQlW2AdFi74p/jVh0XwTLl3OIf7e2nZ7o2TZYtJ6rjfJhIM3Y8lDawHORTqgfm7xU51qQtlcvHeWYaz4jZUYMEj6pbNVtK/ZaizF48ePZZgqjbp27drZXNSJTQq0Im3i6/sYI4ezyplQqSL9zb21HXYIRwrWHq+F1n1T9nWxxYr+UHHqvzbnwLUB4p5NNKF7j176juSzSbQws/5UVYp0we49EWCjQ+hTCwo288dQwBkMwIRZKYkSaEWKMH36XFy9pIlzqZIcCu2m7bBT2rRuK0cMdtxrwtKTffSt1iPk6WN8VUTcv2kmzGtikvmiLcVVsWQqUEC6O+pu2YaTx0/I7Yq4YUt/79690vJmK5/x35YOG1QCrbA6ZcpUxnUvISr3hMU5KUOa6Bf4sbkJU8TP5/PC4mGDqLSh1mRnyFAMqqqJdN7sDEu0HAFPnyJz9erSkm537wGmTEwfmfCsDfOf9O7dW/q/u3TpgqNHj+p7EoYSaIXVoY85KGgpIiKqxjh83d4ICPLHqOAvMByvYgVq6VtThlqTP4T/KBOCx5owZ/5CfatlYNhayREj8P0vv+CH/7rgYRqJhLBl2J/G8F0myKIFHh0l0GkMZi1Lb0t6wgeXkSOn+NlONaFTAhNIhcVwz+JangQHIzKG7bawpDeUQKchShQpCJd+lbCyVwW5OPaoiBXdKsFBLFx30Ne5cJ9xHPebb+Prs3LPinDoLt7fU9tu/h6+Gudz6B61z1jkvq5RC9/DcxnvcRTnNI7ltZm/l8uz4/TrMY4xf+/4NoVx/MRJ/Q4A+X7IKe+BU5+Kzy3OvSvCpdfz29f0rPRsWd1L22++Lfo6F/P3m5/PvMzP4rGrxauxjWVuk9dhdj4uXDeOMxbnvhWR96uYkyQtuNkSjs3FT3e6CWXLlta3xsyy5Q5Y0KnUc/e11bqpaLJ1HnrN7wmnnuUwa3hDdHAYhlU9y8vlH4fh+GXTLEwf2QSO4nqbb5wlt/PYXzbNxvzBtdFo+wI03TIXTbbMk+XZw+o/O/+0UU0xd0hdWR48syNW9K0sy8v6VZWf3dZ5HFb00bbxXL9sno0uSwZgjjjHs/OK62N5waBaz87bt1FuuwqRswRKoNMQhkBTLMMDM2DDqBJSWJd3rSy3Xdr/BU6s+RarepcHIkxwFJWeVcChmxBAIcQerl/ivGtWnHD+Fud3fyl/FHvn58XNU59gy/iiMk/GvQsfwGVQaTy++yZWDyiLYJ/X5Lk3i/2B3q+/INTO/csiPCDDM5H1vvoudkwriHVDSyMi6GV5/OqBZRHw8A08vv2WXN80rph2XiHE8jziO5xa/zXObcuOcPGeDSPF99LPH5NAOwuBM/Yby7CphZDz0ntCaLR9zuJaTJEmbP63CtZ1qYzV4sGR9frbmDq6BNb9Vxku4rNXi2tZK/a9FGKSZRc+qPTzcZ3vHzK9ICaMKwqTuDdO4tzFTnyCdo655PuHi8/M9OB1DBHfN8fld7FenHepuB/8rDXigcXz8vxcN85rLKt6V4hVoJ8+jUThtm/i6RQTznY34dDh2P2a0QWagssffXMhwO899sWoKX9i+LS/kNPrDP50GovyRzdJMZ47tC5mjmgkhfSl8Eg02zxHirbpKcR5ystz1d25FC3XT5Nl5+5l5OLUoxw+8HuItwKfYEn/ang1JATV9jmLc49BuaObsUq817lHWWS9dVl+br7zR5HlthdmioeE/N7is6vuX42/V42S6+aLEmiFXWMItGOPCvC58TZOrs0hRfGYUy5c3JMZnvu+kNt2zcovBZGW6NPQl7B+hCbk/kJ0d84ogINLc+OO+4fCYq2EM5u+xuUDX2DLhCJ46PWuFM1HQmT9hJgaAs3zXD70Ba4c/kyzbI1F/KhiEmhXIWpu677B7bMfyWP4sAh78grCAl7BvYsfiPOWwdNwIYri/DwPr48CfXF3FmydWEQ+fHguvjcxAp3L8z0hnJogGgJN0aTwrhbflQI9bkLR597nJI6jkDqKh9ryvuUwYkoheUzbVbnwy8avkUPck8/uvIVOS39Ak01f4fsL76PbwrzyM0ZNLoSPhEDzs3ieFeIcJvG9nIW4rxLfi+fldvPPM5a4BJp4hexD5R/Ez3eaCVW/e1nf+iKxCfSariXRYNtCFDmzFyOmtsM31zzENZfGJ953UOTsPtTfsVget1RYvaZISOHlfnOBrr17OVpsnPHs3Fwmjv0V2W55SmF/TYgzP0d7f1m8GRSIn/euREH3A8hxzV38LUpLoab4vxYaIgS9uhToygfXop0QdPPzclECrbBrKNDrB1aWAhW1CDGSi1lZNJ9jLD/3vujH6OssP3uP2THPvS/6EsP7npWj3r/6ufOa7zcrm79PlCe1LZIggaYg0urVFs1ijVoXAiqsXwrpqmjvM46Lvo3HGmWeW27Tj+O5jHMax/B48/dwiem8xhKfQJNBJ0rBrasm0r//8Ze+9XlicnHY66IEWqGwcwyBptB2cPgePRfkxfI+5fHXyu+kkDqI8sQxxWR52LRCGDWpsChXRA9xHK3Zzktyo7XLt2jrlFO+/iUs5fHjiwors5AUifmDS8tzGqLM93Zc/j3+cM4prWvDIl4srP8/xDmGTC+gCb84jsew3F1Y2BRvbmsvrpHn/G1NDrQR+9us5ufmwMLBZeIV6MiISHxeThPolS1N8H38YhpRQ6CHT/0LbwYGIt/Fo+K7jcOXt69g3MTW0uXwZmCAeFiUEdvHouKRDeIay6KA+0H0ndsVE8a1Qrnjm5HJ5wF+uHQS5U5swcRxLfG+n7c8zrDI+X7tfpSX7pIfLxzG5/dvIrfnCawWlnLZY1uQXVjWucS+L4XVzOOz3bwkWhltUXO3A+ruXCbP12zTbPy6fhoqieso6eaKl8MjUeHoJrReO0kJtEJh78hOwt6VUO7wZ9L1MHVUcSmmvwnRo+hmuZkR7/m8Kpru5ZDR9xXp3ih17H/42+E75HX/UAosF7oiDAuYgpn/bCb8KcS6wdbsyHP+Aymu3Ecr+OXgl6TI1t2eFSVO/A/5xHn6z84v9/McLweb4ED3RphJ+rtfC3gZH99/Q17Tu+JalvQvK6+xluuX8rOk0CXAgiZumIcOxTWRzp/jxeMNgaaLou+8rngjJAhtXCaK6y6NV8JChVBfxphJv6P0iW14199XbqeLodvifsh55awUUIpusdO70W1RX3lt7FR8LTQYpU/ukCJKt4e5QP/geVKcOwwf+j4UIt8dQ6d3QI5rHuJelJMPhFLiPeyI/Ob6eYye9Adq71qBjiuG4j1/H3E9Xs/82vMG18Z7j32kb5vrSqAVCjvHEOhCpz8SVnMufHrnTdlZR9H96uo7z6zcl4RYUhRrC1Esc/RT9JyfD9X2ZEZpUaboGp1+FAYKaZ0dWWV5zMQiyH3heYGmL3mFsMy5zmWaeChkCHoJfzt+h2+83kWN3Vm0cwrRp0C/LI6nYDsKEX4t6OVnAl1z55fys3iOhAo0abzgM4SOM+HJaBPGjp+kb9UwBHrqqGYoe3wrfjqwRkZT8DPmDK2HsboV3V2Ir0OfyugnrGZGbVBwXYRYlzq5HQsH1ZSiOWJKO/m+BUI4qxxcIwWXFnTxM7vkA0BetxDohtsWYNLYFnLdWOYOqSc/n5YxOyD5XlrNjPjouGIYBs7qJI9b0r8qeizsLcuLB1RHxcMbnp1bCbRCYeeUKFYU5Qt8hXL5s9v98nW2zPq3ihv/iHv46mvNih5ajWlbo0Zqsux56TIuXfZKE0t6yAFtjhJohSIN4Hy7C2Y31ES6VJF8+laFvaMEWqFII5TunlFmu7va34RNW131rQp7Rgm0QpFGuBF0HCW+Ez/p6SY0lDOiK+wd9VdUKNIQy5/WxnC8hukhRRAUqnI72ztKoBUKhcJGUQKtUKQgTPKe7dP3USZfVrtfSuX9ElOnTtW/mcIaKIFWKFKQ8IgItCif/Vl8cHIXx14VETDhdbj0LiMTXj2dxCRYFXFqyNfwGJ4VBwbmxpPxb8JzRBZETnoZa3qXjvE8SVkcepbH8BGj9G+msAZKoBWKFMTSAr2uT0k8Gvsugie8hntjPsDpoV/j2JBccBvyDdyHZ8P+gXlwY/TH8tjdA/Lhwdj3XzhHUhcl0NZHCbRCkYJYUqCZLvbIkO+xrm9JOPUuh039islRgeeGf4Ud/QsJQc6PzWKbhxDqU0O/saj1zEUJtPVRAq1QpCDmAk2BdehZSb7SLcFF2669aiIYlSva2M5t5gu3mx/noA9DN1+MY823RX+fXDf7bGPh+bjdOEfUogTa2iiBVihSEEOgN/cthsAJr2NZzypw7l1WWL7lEDrxFawQwvd0sglHBn8H1/4FcWv0R1Icvce9g7BJrzwTzN0Df8TN0Z+I4yvL90C8Z6XYzvXH4zNiY9/izwTWdUAB3Bv7nvwsn3EZpXUdMell6bem0F4e+bmwurNj/8C8uD7qE2zrV1ie7/iQnNgkzvNYvMehVyUs76F9Dj9PirYSaKujBFqhSEHMLWgK74oelYEpJtnBt2dAPimAdFfcGZ0JYbpg3xYiHSTE3G/822JbBmnp7hmYT4j3J7oVXFEX6Ary+JgF+n0h0JV1S1g7nu4QHu85IjPch9FfHSXQ98d8IN9LIfcd9/Zzn8OyvH4l0FZHCbRCkYJQoH+tkF3mrHbqUwmrehsTEmgLt0WVtVfzY7jf2G5+bPRjjHJ82/g+43zGNvPX6GXzz2HGvWHDR+rfTGENlEArFAqFjaIEWqFQKGwUJdAKhUJhoyiBVigUChtFCbRCoVDYKEkW6Dt37mDUqNhDbAIDA+Hr6yvLBQoUkK8GWbJk0UuxU7x4cb2UcLJly6aXEseYMWP0EvDrr7+iRIkSKFasGB48eIAbN26gevXq6NChg5w+aNOmTdi+fbt+NNCyZUuEhITIcsOGDWUyHG5j2Xx6nuzZs+ulF/nvv/+QO3dutGjRAsHBwfrWKPLlUzNkKBTpkSQL9OXLl6WY7d+/H2vWrMHo0aOlOBmUL18ev/zyC3x8fPDhhx9KMT9w4IAUvCFDhshjpkyZgqVLl8qywb59+zB8+HAptseOHcPixYsxfvx4+d7+/fvj4cOHmD9/Ph4/fgx3d3f5mXyPk5MTJkyYgICAAKxatQr9+vWTAhseHo4RI0bIz79586b+KVFQRN977z0sW7ZMrmfNmlW+Ep47Y8aMCA0NxZkzZ5AjRw4sXLhQXpPBN998Ix9G5H//+5/8TszwZS60vI4BAwbI8qxZs7BgwQJZJhT7N954Q34/Phj8/Pwwc+ZMuY+ftXbtWsyYMQNeXl7y4TB48GB57idPnmDgwIHo3bt3jKKuUCjsn2QLNIV57ty5UhS7du2q74UUpI0bN0qRowDev39fChjX33nnHdy+fVuKMIXJ4PDhw6hdu7Y8lkI5bdo0KbRBQUFwc3OTwvzll1/iwoUL8rMomBTDzz//XFq3H330kRTDkiVLSgv/gw8+QOvWreUDhBb5rVu39E+Kgg+Do0ePynOQr776Sr6/b9++8mFSoUIFuZ289dZbUpxjE+hPPtFmYaZFnCtXLvlwIPzO7777rmxRfPrpp/KhZsDvxvtDkeU18j158+aFv7+/PJbWOT/D1dUVHTt2lA+tUqVKyfOfPHlSPvwiIiL0sykUirREsgWalumePXtw8eJF/P333/peSOGmJUhRpHCSH374Qb5SrChaFNr333//mcBRrMuUKSMtXQo0xZfCRDJkyID169c/O9dnn30mhZdW59ChQ+U2Q6Dr1Kkj1/k5R44cQdmyZaUVTmhpm1ucFN2ePXvip59+wu7du+Xn0krnwmvk5/K70eqn24IPCT44Hj16JK11ukJWrlyJdevWoVChQnI7j6e7gpa9AR8WtNZpifM6DfcP4T0gRYsWlYLMe8ttW7ZskdsNgeZ3oIWdP39+eW/q1q2LJUuWyGMUCkXaI8kCTXE6fvw4PD09pSixyX369Gl9L6RVx+a5t7e3bJoTQ2w3bNggxY+vtALNOXHihBSmbdu24cqVK1IoyalTp6SAciFs8hMKljHNPD+H7gha4oTnpzU+b948KZgUM7oE+GAgFEkKOKFo79y5Ezt27MDq1avlwnNxO8WXVja5du0aXFxc5H7j+/Ja+T7C+8Djze8FYWuCAs1rNM5lwOsk58+fx71796RVzVaGAc/PBw+Fmxb2rl27pNDTPURRZ1mhUKQ9kizQ9gKtcbpJpk+fLtcpdrYOfeZ8sMXF2bNnpeW/fPlyfYtCoUhr2IxA01KmRZ5caKXSEk0sd+/efRaNYSnM3RgxwVYIO1HjgtdE61mhUKQ/bEagP/7442Q11emfpe+X/mzD150Y6DawpBC2atVKun7iYvLkydL1ERd00bBTke4hZ2dnfatCoUgPJFugjYgCho6xTKuRnVokU6ZMUjAZB81OLzbb33777Wf7jCgHdi6yQ49+ZpPJJGOCGUHBKAa+t0aNGtK6ZrQDOwcZucCICaMTjXA7ox+uX78uz8H3FSxYUFrUmTNnlpEZPI8BO/wYptelSxfZOcmOO/qN6TZgZx8jTugDZ5nXQh+2h4cHunfvLq+Xvl8ew3A/fh5jlekPJ/S/8/sRw5fM703/9RdffIEff/xRdq6yo2/z5s3y3jFOmt+P0S3VqlWTx7ATsGrVqrITlNfx7bffyuPZSUh4zxQKRdolWQJNIcqTJ4+0fhkFwQ4uiiDjc2vVqoUePXrITj8OTKFA0UrloJCxY8eiTZs2+lm0UDMjnO3VV1+Vr+xI++OPP2SZ7+V5GPrGMDOG8DHsjnHRBp06dcKlS5dkpx6vibz55puyU65IkSJyoAnD1Ax47RR0PlwI9587dw4vv/wy/v33X3ksBZtCzPC3Jk2aSNHkQ+Wll16S+7nQauf3N4dCbQyaYXz1b7/9Jjv0GPXSrFkz+Vm8R4wGYeciRZvs3bsXnTt3fm7ADbcx9nnFihWyY5JUrlwZgwYNkqGNCoUi7ZIsgaawUjxp8dK6I9999518pfVH65WhcK+//roMn5s4caLcR4uT7zWgL5bhcoT7DGgFv/LKK+jVq5cU7G7duuHgwYPSyuU6IzIMGILH97IT0LDgjXMxXprn4YAPc3g+Iza6bdu20oKnZctjDdFllAoHwFD469WrJ7ex05Hhd8boQKNVYI65dWscx89iS4Ln58OEgsvwPYo07xGteLY46B7h+flgoEDz82jt8/vQ6mYrxfw+KRSKtEmK/8ppaf/+++/6WtqFDxIj3M/SsIXAwUEKhSJto8wwhUKhsFGsLtD0FVsC+nrbtWunr0XBjkcOiybsVEwo7HyLKcqC8cVxYYTjcaHbJqFw6Pmff/6JrVu3yugNS8LzKhSKtEeiBZrCxIEUhB1+9DNzqDM78DiKjlCA2JHHkXmMTOA6Rw4OGzZMJgsi7OBjRxcjIwz4HubYMMLtOAiD/lf6fydNmiT9zBydyOHWzKHBz6b/u3nz5tKnS181oa+bfmpjlOC4cePkZxsjGtnRR/8zX+lzpi+bYWwUbHYSMrKDsDOT/mdzmAuEHZyM3mBnHj/HGDXIEYFcjx7bPHv2bBn9wc5CfmdeF0cz8nMOHTokj+E94jVylCKjNniPeRw7E/ndifE9OOiG5+GxhNdonmFPoVCkDZJkQTOc7urVqzKaYM6cOfj555+lwDCvBbexY4sj+CisjJKgqLPDj0LGyAUKKI9lSJk5TFREkWckB6MeKHYMm2MiIwo5LUVGTrBTjSLN89CfzRA8PgCYeY4wDM84j4ODgxRjnotlA4bdsaOSnXM8lmFxFHx27nF7o0aN5AOGDwSmDzVglArD73gMO/8o1PxcWsa8L+yINO/A40ODAs2WBEP12GnKjHe0qHk9zGTHWOj27dtL0eWwdIYQ8oFDGPvM3CIMr2O4IC14RsXw/TyO18wOU0bNKBSKtEWSBNqI/WXEAVNiMnyMrgEKHcWaVjJFlKFsjExgaByFm2FhjJZgyBgt6+gw3IznoRVLa5ciSWFiOBwFiwL9zz//yDI74EaOHCmFbdGiRdL6NaIpjMx0RlIiWrq0VilmBnRPUGQNUWcUCkWe56DgM9aZYkvRpLgbMDqFljwfLkY4Hz+HOUIYv8xRjOYDXtgC4GdT6Hmf+L2YRIoPAoo1BZr3kaJrhAEyvprQUub9orAzXI8CzXvKSBla/7xmfid+Nu+LQqFIWyTZB82wLwPGD1OQDV8wm+20ogmtZiOagdndDHeAkfTInK+//lparQy7I/wM4zzcRvGjL5rCylhjWvEULDbvKXKMsybGe5hlj/spdHQNGGFyxLC6+XmEURdcZygcvwvhdUcffs7WAEP5eA2Ge4KfQ3htvJboLg6eh8fy+3BIOwe+0BLmPaCrgy0Nhs/RhcHJAcyz4PH6+DBgC4LbKci8Vr4aqVop4PENGVcoFPZHkgXaGhgJjSwJhZs+XLpDKNa2CEWfrh8KtJGZLzEwy51CoUh72JRAKxQKhSIKJdAKhUJhoyiBVigUChtFCbRCoVDYKEqgFQqFwkZRAq1QKBQ2SqwCfd5ZnzYqEjg05qBW1okIjcDdk3dlOfBRIHb2dsW+oXsR8libMmrPwD0ICwjD/TP35fp5Jw8EeUelF3VpthrhQXGHkz25qw0btwah/qF6ScOpoZN8dazjKL9bUjkwYj8Wllqorz3PwwsPcWicFjdtwHuye8Dz8eAB97UYcAPnxtq1KRSK9EeMAu217TJmfj8DeCr+j3iKRaWfFx2KysKSC2TZ57IPtnbcIsV5xnfTERkWiZm5ZyDYJxjjPx0nhXZH1+3wu6bNNhIZHokzS7VcG54bPHF+9flnQu615TKuul7BXbe7mF9kHq7suIJbh27iith2bdc1XFijzcZ968gtKbKe6z3hvtIdd47fgbvDOfjf0gbKPLrwSK6HiYcAr+/20dvwEA8J4tpzB3b22vmcEM7ONwsRIeE4t/ys/M5XtnvhnNn5vD295flCA54X9sAHgeI95/DkzhN5TTN/mAGfK1EDRkKfhOLcirPyPJc2euLB2fsI8Q+Rn3N8xjE8vvkYa1utleth4tz8zFX1V+L+6Xv6GcS15Z8l79NtcX5yT+xzX6FdCx8mfA+/o0FYYBjOivPxs8hV16viGs4h4J71HngKhcI6xCjQFF+/6344MfM4nkY+L9BcX1FtOU4vOiWF1RBosrblGjy+9fiZQG9osx4z88zAxj83PBNosrzqcnmemd9PF1ZkMOYXmycFc0GJ+fKcYUHhWFFdO2Zbp604u0TLMDeviJYD2bXHDvhd9dU+xy8Yk7NOQohfCKbmmCrE7T6Wi+uj2E/KMhEXXC7gsLBcr+64Ks/l7ngOlzdflkJsQIEmi8suQmREpDjPFCmuk7NNwgOPB1hScQm8tl7GlOyTcfPgTfH5rkKcA+R344OCIkphnFd0rjb0ut8u7BfWtGtPV5yYdUIee0+0OA6Klsj0XNMQHhyGGeK7+9/2x8q6jlLg5xacAx8vH+wQDxB+bwOemw+55eJ+BPsG48G5+/AUYr+g+AIcnXJEWu0UegM+IPmwmJV3pvwucwvPkfeID0+FQmFfvCDQtEZX1FiOTX9tlGJCFhSfL61FLsemHZVCvLn9Jiwptxi+Qig3/LFBWGwPMD3nVHm8IdAb264XghGBqV9NeU6gDfE1hJFWI4WOlu+cH2cLAQvHwlLiISHOvfXfLc8EiELOz3Oq7yT3zf5Re78hPrxeihOvhw8YuhDcHd2F9XpJiuHGPzdK143bXLfnLOhZeXWBFt+HojY7/2y5zu9BV86aFi7yfIEPA7VWhbh2Wq9zCs6W1vGcArOFBR6B+UXnyfdxP5cAcb8o6AtLL8DD8w+laB8Yvh+ONR1ky4HCu0V/uPG7PL7xGOt+X4fH4rMMZuWbKV+3d90mhXz6t1Phscodc8Q1stVy79Q9KcYGjrUdxPc7Ke7VfISLVsGyn5bJ7TxeoVDYFy8INIWD/mNyffc1ISL+ODn7pGiSH4fbPDecWXLmWdIhNq+DHgZJK9FwP5DTi09Lkb2yw0uus1kf4qv5pwmtWp7jzBItLwddFRFCyHnuG/tvyG10b3iuv4hre6498xlT9N3mnJSCS3EyXCWnF2nnOb3wlHy9d+ouToprogB6X3wE3yu+0iK+Ks5JgeVx5g8MWtvhwmr3WOmhXVe089KqPznrJPxuRL2H8LufFNdDC5nQlWAOHwq8N0E+QVLc6Wq5eeCG3EaLmddF1w3hdyd0xdw6pLkziLH9+t7r8hr5fs91F+G54aK0qI+LVk7AvaiHTbBoSfCaHokHwpP7T+Tfk5zVv5M9wtwqxoS8CkV6ItZOQoV1uL7nOjaIloUhnIr4YUZDJplSKNIbKSrQocKSplVJ6G9lB2RykG6XR4H6WuKgpWweWWJLGJ2TCg1mDzRP4apQpBdSVKDpQ35w7gG2dNiMi2sv4Kl5T1001rVep5dihuLq3MhJ+qQNnBquwrKqS3FkkjaTysTME2WUxPnVUbO2GATeD5SdeJaE/mbDZUHoA2ZIoVP9lVhUNubwu5g4MFJLI6rQYMrV+/e1qBSFIj1hPYEW2ru4/CLMKzQX27tsw9qWazEtx1QZQcHoiFV1V2LPoD0y8sFjpbv0QzOKY17RedK65jHzCkfNXE0/LjsV2dl1aZOnOPdi2TkY9Oh5K5gdmAwzI5OzTcbSyktk56MBOxzZqcaIEEZb0NfNz51fbK4U+6UVl8h9jASJDvexc3BJxcVyfa64vhsHbsjOSYeaK7Dsp6WYlXum7Gg1Z1mVpdIHbsCIEz6s2BlJXz33029OvzRFfurXU2TnJL/v+ngeVOkB5tu+dy8q9FChSC9YTaDvn70P115aMnwKDTvJ1v22Vq4vLrdIuhgYrcBBIpc3XZKiyQEvO7ptl3HYFE1zaFXePakJ3/zi83DH7Q5Ozjkh183xvuwtRdmA4W/Lq2qRDIQC7n/HX1rQHFDDMLadvVxl6N55Zw8ZsbKyviM2d9DmLzTn0cVH2NppK/YN3Ycd3bfLgScUVLcF2sS4Hqs8xMNDm6rK4PKWyzgx6/mk/4xRZujerDwzcVcIMx9moz8YhZDHwXL/7LyzEBEWiY1tN2BXP+0epmf2798vp/hSKNIbVrWgaR1TjBl/TJfEula6QJddRCcw9goLmlYpRc9tvpu0XI1YZ8ZOLyi54FlECd/PsDfup7V9+9jtFwSaFvcCId50cfABwFjjOQXmaHHPOvdO35WW96IyC6UFzciLuYXmyLA0hsbxQbGyzkq5LyYY/kcYGshBNxToU3r0CEMNKbocnEIYssfYaYa6MYTP4PTC01hSYbF8kHAQCsPzGAnC65Lhh3lmSVcQ7x2vK73DGWmiz1+pUKQHUtQHbQ+sqrcS69usk+4ZhW3Aacc4FZlCkd5QAq2weTgjOmd3VyjSG0qgFTYPZ3r38tIGPSkU6Qkl0AqbhzOac/ZzhSK9oQRaYfNQnN3d3fU1hSL9oARaYfNQoE+d0iJlFIr0hBJohc3j6ekpIzkUivSGEmiFzXP58mUZC61QpDeUQCtsnitXrsjRhApFekMJtMLmuXr1Knbtinlkp0KRllECrbB5OEhl+/bt+ppCkX5QAq2weW7evIktW7SpwRSK9IQSaIXNw0RJmzZtwpkzZxAeHq5vVSjSPkqgFTbPjRs3kCNHDhw5cgSFCxfWtyoUaR8l0AqbZsCAAfjnn3+wdq2WqjY4OBiNGjWSZYUiraMEWmGTHDhwAFWrVpWCzPkIV6xYoe8Bzp07hwkTJuhrCkXaRQm0wqYIDAxE2bJlcfLkSX0L8OjRIyxZEjVLDpk5c6ZMQ6pQpGWUQCtshs6dO2PcuHH6WhTe3t5YsECbycacFi1a4MmTJ/qaQpH2UAKtSHW2bduGn3/+GREREfqW5/H19cXs2bP1tecpVKiQXlIo0h5KoBWphr+/P4oVKyaTIcXF48ePMX36dH3teTj3JM+hUKRFlEArUoW///4b06ZN09fihkI+ZcoUfe1FfHx88Pvvv+trCkXaQQm0IkVZt24dGjRooK8ljICAAIwfP15fi5ljx45h/nw1A7oibaEEWhEjDG1j9AStUz8/P2nFUigZZcHQt9DQUDmqLzIyUn9Hwjh//nyc1nBMhIWFYezYsfpa7EyaNEmG4CkUaQUl0IoYYQgbrdKDBw9iz5492LFjh8yHsWHDBri4uGDlypUyNnnx4sWYN2+eDHujy2LixIlSTEeOHImhQ4di0KBB6NevH3r16oXu3bujS5cuaN68OcqXL48///xTuiZatmwptzVt2hQNGzZE3bp1UbNmTVSrVg1VqlRBgQIF8PLLL8v3lCtXDhUqVJBLpUqV5H7GS/NYdjRmypRJvtaqVQt16tSR56pfv7602nluDnJp0qQJmjVrhl9//RWtW7dG27ZtpculY8eO8vp69OiB3r17y0EyQ4YMwfDhwzFmzBgZe82Hy4wZMzBnzhwZWbJ06VJ5H9asWaPfOYXCciiBVqQKFGZa5gmBVjoFOqF+5lKlSukl68HOSV4XI0+4qBwhCmugBFqRahQtWlQKXXxQ/GiFv/rqq3B2dta3xszUqVPx77//6msKhX2jBFqRqlCk44MWKl0OzGpnMsVcZel75ghExkwrFGkFJdCKVIVuDvqB44JWdrdu3fS15wkJCUGNGjXg6uqqb1Eo0g5KoBWpzqFDh2Icym0Oh4FHhx14dH0oFGkVJdAKm2DUqFFxjihkylGD06dP4/3330f//v31LQpF2kQJtMJmYDgcY61jon379jL+muF1R48elbHR9Eczib9CkVZRAq2wKRjzHBNZsmTBwIED9TWNs2fPSpGOTdQVCntHCbTCpmDERunSpfU1yEEyHHDy119/6Vueh+lJ6e5QKNIiSqAVNsfDhw9lLDPD5mglk99++02+xoTKCa1IqyiBVtgkd+7c0UsaHA6uUKQ3lEAr7ALOnhIfzJURX25phcKeUAKtsAt++eUXvRQ7jKdmp2FsM7MoFPaGEmiFXcBMdwmBWfOyZcumrykU9o0SaIVd0LhxY70UP/ny5YuzU9GcfUP26iXBU2BJhcX6StJYWccR2//bqq89z/Zu2+F/019f0zg55yR8r5jlDxHXEOIfoq8o0jtKoBV2AXM5Jwbms04I8wrPfZZR7/7Z+/Bc74mwJ6G4eeAGzi0/i1BRJtf3XMMFlwtSQM25ffQ2PFZ54GnEUym2q5s4IzwoKvUoxVeeJyAUZ5edlfu8L3nD3eEcjkw6gr2D98J9xTlcWCvOLdjcYRN29d2FIO8gua5I3yiBVtgFHGVoDcwFOjI8EgtKzMfjG4+xuulqae3OLzYPx6Yfw/au23F68Wksq7oMR6ccxQ6xfm33NWEtb4PvVV8sKDkfD9wfYM+A3Xga+RTbOm/F2SVn5Pmu7Lgiz72x3QY8vuWP6TmnIeB+ABYUn499w/bhkngonFp4CidmncDx6cdxZfsVeQ6FQgm0wi7gzChJYevWmN0NBhRo/9v+eHLHX4qiIdCuPbXseHMLzcGhsQelKD/0eIiI0AhERkRKwaVV7dpjB+6fuY+FZRbC+7L3M5cJ90cKq/rhhYfSst4rtm/+ZxOe3H2CFdWXw7mRE3yEJb1n4G74ePngwdkHODzhMNzmuuHMotMIFAKuUCiBVtgFtWvX1kuJg9NbxTZ8nJx39sCp+W5wEyIaERaB86vPS7fGrUO35H73Ve7ylVawdFEEPz9zCl0cdFfQCg/2DcadY8/Hb985fke+jy6Q63uvIywwDGeXnhVCfBJTvpqMuyfvIMQvBMHewbh/+p48z9mlZ/Dkthp8o1ACrbATOEdhUmEejz59+uhrqY+HeChs6bAZD8490LcoFDGjBFphFzApf1JRme8U9ooSaIVdwFm7kwNHGC5fvlxfUyjsAyXQCrugSpUqekmhSD8ogVbYBZUqVdJLycff//nBIgqFraIEWmEXVKxYUS8lnzfffBPz5s3T1xQK20UJtMIuKFeunF5KPr6+vrLT8MqVK/oWhcI2UQKtsAvKlCmjlyyDq6srMmTIgJAQlfdCYbsogVbYBebTYFkKxkbPnz9fX1MobA8l0Aq7oESJEnpJoUg/KIFW2AXFihXTSwpF+kEJtMIuKFKkiF6yPMx/wU7D+/fv61sUCttACbTCLihUqJBesg5OTk547bXX9DWFwjZQAq2wC+LKSGcpmjdvniKfo1AkFCXQCrvgxx9/1EvWJXPmzNi1a5e+plCkLkqgFXZB3rx59RIQ5BMkE+IT5lcOuBcglicvTEdFOOUUj1Eo7BEl0Aq7IHfu3PKVYnxw1EHMyDUdof6hOLXglJyt5PSS03KmE3OYJH9r563wv6Xl3jBEnXD2FDkzStjz71EobAkl0Aq7wBBocnrRKczKO1OWzyw+g/lF58mpqjgjisHGdhuxutlqzCk4Wwr0wlILsL3LNjnH4KUNnlhZ11G+557bXf0dz+Pz0AdfZvlSX1MoUgcl0Aq7wFygya4+u3DjwI1nbo2tHbcIsb2nrQgmZZ0oXznZ663Dt7C4zCJhbbvJ6a0enn+IOflnS7EOevT87Nnc51jbAet+XYsKFSska6IAhSK5KIFW2AV58uSRr/dO35MTvTrUXCEtZs6APbfgHKxu6vzcTNhnFp+WIsxJX5/cCZCzbM8pMFtO0sqppngOWtBe27zk8YdGH5SzbU/OOgmTMk9EeJA29+C7776LWbNmybJCkdIogVbYBZaM4uBErYvKLMTisgvlpK7k8uZLmPjFBEzJPhnb/tsmt5GAgAA5iMXPz0/folCkHEqgFXZBwYIF9ZJ1WPfbWukimfDZ+Bc6G8PDn5/JOyFcv34dgYGB+ppCkTSUQCvsAmsO9XZqsAphQZYNxduwYQNu3bqlrykUSUMJtMIuKF68uF6yHPRhr6ie8Ilkvby8MHToUH0tbpIr0Jac4kthvyiBVtgFpUqV0kuW4ca+G3Dt6aqvJQy6Opjkf/369fqW2EmuQFsj/7XC/lACrbALypYtq5eiuLH/Ou7GEsccGxyYsrrpajx0f6hvSRwUXXYaPnwY9/vd3d2TNTmtEmgFUQKtsAsqVKiAm/tvYmunLZiVe6aMuJicZRLunohfoJlO9M7R21jfZj3OLDmjb006K1aswOuvv47ISOuNQlQTFCiIEmiFXVC5cmUZ53x64WnM/GEGJn85ScYsH59xDIfGHcKO7juwtuVasazBulbitdUarGnugp09XXHeyQOhAaH6mSzD4cOH9VLM3L59O1nzHXJi2+SgYrfTBkqgFXZB1apV9ZKG/x1/KcjBPsH6FtuCfurUiuJgi2HcuHH6msKeUQKtsAt+/vlnvWRb0FK+dOmSvhZFcjsJa9WqpZcSjxLotIMSaIVdkBzBsibsDGSnYXDw85Z8akZxUKDHjh2rrynsGSXQCrugbt26esn2oBh+/PHH+prG8ePHk+VHTm4Uh5pfMW2gBFphFzRs2FAv2Sbly5dH9erV9bXko6I4FEQJtMIuaNKkiV6yXbp06aKXAB8fnyTl8DCIya+dGJYtW6aXFPaMEmiFXfDLL7/oJftgzpw5OHPmrL6WsqhOwrSDEmiFXfDrr7/qJdsnLCwM3+crgGbNmupbEk/Lli31UuJRAp12UAKtsAt+b9VCL2kwN39IBOAbAlzyA47dB3bcApwuA3PdgfGngBEngAFHge4HgX/3AX/teXFpvxfovB/oeQgYdAwY7QbMOAc4XAK23gCOivPy/PycUPF5QvtiJDIiAhFchDh379IF1UcuQY7qzRAeFiq3RUZGJGrkoYriUBAl0AqbIDAcuPEEOHwPWHAB6CZE9bedQIMtQPUNQLYhR/CXENNeh4FJZ4AVnoCrEOSz3sBVf+B+EOAfCpjNC5ss+AB4Eqadl+c/Iz5n201gyUVNxLscENfnCvy8EagrrvHzvxbitY8zo+7MTag/azO6ezxFl1MhqDdjE2pOdML777+HY0fiHn1oTnKjOK5du6aXFPaMEmgbITbLLK1wOwBYdxUYLKzU+kLQqqwHam0C/hGW7aTTwMbrwEVfILZJttv92VYv2Ta/tWqFJgt3C4EGepwHynUfhwb/jURN8Z2rigdNV/HgWSZE3uux/oZYUFEcCqIEOoWhRWY2dZ6k0ErRPBfWmT1DAd4iRLaPMBKbb9es3pbCAh4oBHmtEGa6CYKjJt1ONO3bt9dLts0aZyf8veeOtKJbrT2L2pPXwPvR85nv+DCmVe5yRYj4IaDhVqCeEPCO4mG1XLQMvMS9On1KmOnJwMnJSS8p7Bkl0FbEXzSRaTHOFdYUyTRP/AhFM900RWvSE4padWFN/ipEzdahdbv3DjDyJFBnM1BxLdBiBzDDHTjnrR9kJf755x+9ZNtky5ELX/1YBDOmT8cqRwdkK1kFtRM5CpKunrkXtJZGhTVaK4OtD6POxIfqJEw7KIG2AEazvIdovn4wFyi1Wls3TQWuCUvphp4W+JP5wBghbu/MEj8isU5/6ZeLgFPCwHpzhu1Y0XcCgfXXgC7i+9AN8Yt4eNDveuQ+4JP0BG3JolOnTnrJdqEwOjg4yLL5UO9JkybJ18TQrt2fekmDk4yfeAAMPQ40FhY3xZudoPSNR0cJdNpBCXQiiNBdEw+DhCV5WytTYK8+1kR5SrRUw1kXA8VES5ORBcTFC6i9EWi2DSjpLJrDoonbUligjmL/q0KgU9oNzU61TcKCZwQDO7u4UIhPigeGrfnEu3btqpfsg+i5OL7++msMHDhQX4ufhHYSPgwG5okWWm3RouHfb9wp4ILvU4wfp6I40gJKoBMIrV3TNOCusC633dCsY/qS35kNBAvr5iWxj5Y0hS2bEO3awvIkj4UIMsSrjBDwX4UYjxECeNEHeF0IsjlrhVjzPNbCXXzm1LNAU2EN1xU/5n5HtNC0AMvOlWo1evTooZfsg/379+PRo0f6mvjbBgfLpEqHDomnYQJIThQHW21jtl5EE2EI1BN/61nuWh+Bwv5QAp0ITovf2//mCytTNC3pSy66SgjtTG1fPtGyddRH51KkXxMCHBYBzD8P/L5TCKNolpJ/xPv+2y+E0UpizKbwHmHds7OuprComghBXiCu4Zad/0B79+6tl+yXs2fPSpEOCIj/j2HJORjZGKJ7pOsB4KcNQF/xcOZ69M5qhe2hBNqMM0KAbz4Rzf5rwGcLNDFm54w5jH19dboWJkWLmBY04aAJ+pg/mqdt+1cIMV0i++9az3qhdb71utb7X2Ud8PceYOdNwNeyk4fYBP369dNL9gFFmANXojNx4kQULVpUX4udhFrasbFunagQcXBPtATZec0488bC0nb2sp/WVHoizQt07hV6wQzG29IPPEM0+U8KSyLLQm07XRMcnGCaDCwSVid9el8t0faZQ/eE4Y6oFvfvwGJQjHfe0twltII4Ao4RIIwUSQ8MGjRIL9kHnFHl5s3U6fVNSidhkHiWsE+EnY+NRGtvtRBs1jlF6pLmBfo1Ye22F5YlO/PoO/YO1izc0EjN7TD5tDa0lz3j787R3vPhXGD3bS2syTWG39gTK1dcDiveIKz4truBSuIB8J9omnKE3RMr+qhtneHDh0vhsReSm7D/33//1UuJxxJRHGwR7rujdWL/tB5YfAHwU4Kd4qQ5gd4ohC2zsIjfFSJ8XFjHtILpsiCMlKAb431diGmR1hDWKGFFrKWX6cdlaFnbXdbvXOHgDVrxzBfB0XV/C8t4u3go0JJXRDFq1KgYXQa2SkIEOnPmzLEOyU5uLg5Lh9mxk5wGDq1rLptF641Wt8K62LRA51mhWZMG7NRgpMREYfWyQ45WcSZh7UYfodbaFcixVHNvMDqC6+TrJVoPNzvtsi3WfMwPgrR9JCUsBEZTDD2hWcatxHWsuQo8ss15T20KJv9JTn7llGbnzp3xzmqyY8cOvPLKKzEmUUpuLo5Tp07pJevA1iXDRjkCksYNBzCpPkfLYxMCvV6IFIc7Dzqqb9ChBbtSCDED8keJxe2hZgVf9tOiJ8JFjejN5DlCsA0Yc8wkOxRb0wTtlSFwFHNGNqQk7HBkRwzdJ3U2ATPPaUN8FYmHnWuhoWmvjd2xY0d8++23+loUloziSAnuCUNnmqjfdId02s9YbH2HIlmkuEAvvQi8L6zel6cDh+5pI9MY/UBKu2idEwYH7wJ5HcSxQmAJXZAZ9HLltdpgEQ4S4TEGjJygxdz/iBazHFvyHUtDi4LXzjwUNYUYj3TTMq0pq8IyTJky5YWJWW0Z5oROqM88R44c6Nmzp76mwU7G5ODqqjcbUwkaIkzfypbi8ONaDhpF4kk1C3qksIi5MKLCiKI4IJpJBRy1MmFHnhFRQZ9yiBBBuiXuBGidaBxaTWiBpyQUYzbpGElRbYOWenKXeFhYc6BJemf69OkIDBRPXDuBApuYTkJLdoBawwedXJhX+8/d2sAZJolibm1F/KSKQHOIcTVhIGRZpFm8HJXH+kmB+0JsM4dxxfRDnxdCTlFmFEZKQ9dKH2GRMzlQ651adjYlxinL7Nmz8eTJE33N9kluFMfQoUPlzOBJwRYF2hx2OC4SLWnG7tPIoZGmiJlU9UF/LixnD28tHvkLUWbMcfSBISkNKwuztXE49K+ilUiXDJMHKVKXefPmwd/f8g58Ggi05hhWZr6w9ZYcmzapAl2nTh35mjdvXuQpVESWE4utC3R0OOiLoxsZUcXJGMwDA9I7qSLQtJ7fmKll5kpNmGhm1jlRMTZqIW6TReW4ZT9GWrpiycL5CHwcZWox8oW5RFZe1hIEMfMeU5+yk6qysMxonVUVC/NSNxfbOwhLre9RYJR4+PLvPMddmx3FyUszCoyFWfy4sJXEDurF4hjmsphwWvOpsgOspXhws5+hqvgs4/NYpznKlDO+TBMGx8BFW3Dw4t1ED6du0bw5ihYtgqylqqHSwNkITMCw8Jg4eFD3/9khzOrIdLb1xcJQ2PRMqlrQKQmf0hyQ0my7FhpEK/m8j75TYROww9jtkZa0fqAQ0za7tOmkmPK09OxL6LQrWOY24SAiTgDAB6ylpriyNIHCCmcUz7EH2vyGxvdhEi2O1uMgpLFumgAx//P27dvx6quvoFL/Gfhp0Gz8e8RPzspSoe80VBo0B69+9IXdjaa0BKwTfKCyr4dRWAyTTU+kSYG+Lv6Is4XVwx8CpxkaKywshuYpUhcOvmHkDv82zB/CQUS0QOnXZ6pWjlyLbej6iuXLnssOZ+skdIJY9r14CEOBD6XeokVZpkkHVB++SIozl9/WnUX5ipXEkYl7EtmzBR0XnBiC4bcUbLaAUipKK7Wwa4Gm9UQLhQM/aGUxvwZTatJaTo7/MLVhSJK9Xj9dDxRaplXlAAb+kGg5svXCiQlo9SYFJsJ/8ED8se0EJitKSi6OkKBAVBYW8z8HHqLFyuNo53oD/0xbJ10rtL6bijo+QRgcbGnE1nqwNx90UmE/gZE/5HdRx/jwT2vYjUB7i6YOh2wzVWd1YXlxMAoT3afWDB+WgM10poA8cFffoMNUpbY8oIUda57i2pmfgU31n/VmO5vszN6X0KmZEgPn2Lt3z35+gUntJOSksz82+RtlSpbA8WNHkatMVXyd63t9bxR80NH/zvtvPATZoc16Q4GeMD7tC3R0aBwMF8Ya+x9GnIQMx7V3bE6g2QxmjDF9dsxn3FBYDMNE0++0sL4C7Tw/BbPP8Ttx+n6mduQAHDnicYp+gOBP8UNjZ9doUcFsAQrxIiHEf4gHIjvDKATLRHP8+hNNqFOKNWvW4O7daE8yGyapAt25c2f5aj7Uu1ixYnopbmhRXxGtx0mnn+L7NuOk/54dlpyENj3CvDt0hzAIgOlU7dEdkmoCTSFmMiO6JJiYiFEUXQ8KEbth31mzmGeX0JfK6a7em6MN877kC2RfojXLjCB9hhVxCDqnxmJvP33nFddow8M5MMfaE7Gaw5bIDqEnHHTD6+JDgh1ytPJTUohjgy6D27dv62u2z5YtW5L1QDEEmtbw22+/jTlz9AxfCcR1h/hR6XDYNV1O9Pfzt7ZMWNo304B1mRiYr4eGBaNt2olWByOA7MGNmOICTdfEAGEd019kz0mCmPHukT58daEQMvbYE9N47ZVpTj2jBeAznel3y4EV+swrpZ21iVjpumEiJ4Z+TTyl9VRzei1rccFH65RjrDd99/x7cDCOtWZ5sQQbN25M1sAPe8Pcgn78+LGcieXy5cv6luTBHDYXxYOXf3cOxWYIYnQ3W1qH2sPfAL9/N2EY2upgGbvuJExNmAXPmJeQM6vQ4iVG3hBDYOkHY8a9Lvu1dfpnaaEyARTTNvKJXlf34ZpzSPxgkjslES115gOhX45WPGfPmC2sc3ts8m7duhU3bojmlZ2Q0CiO2Ig+Ezgz31GkmeMjIZw5I9QnEbA+z7+gRdZwLsNV4llgzwZUYmHILfuDGPXF5Gu2MoejEugEQqGNnqOZ4WIU2x8dgb6HtR727Iu1fZwUgCJLOAv4x/OB48Ja5oipTxcAu3RjkL5cS/wQ6F+jy4i+ew5J52AK+t2YZSwtQIGKLXeyLWKNGVU43N3HJ/7gfUtEcdCfzfr0zz6ggqhPHOHH5GPpBboXOVEGvzsHKaXWd093Ah1fRwHzhBg+YrogCIekM0ysyErNf2fO98u1dKaE+asp2ORRiJalj0umeVqPO61n5oNOrk+XQ5HpkmATlaFXLYQYr/AUT/00/APavXs3rly5oq/ZPsnNxbFiRQxztSUQa4XZMeER49dZxxmxY+8TEScGuiLpCmILgx2v91Pot5auBJrNls+F9Rqd+aLZX1CILyMn3ITVYLgrOPMK3/PGDCDnMm3YMIf/msNoDM5RSCj+5rmpLQHdHOyNphhXXKfFe9IyTm/pG/fu3WsxH2xKkFyBji9hf1yZ/VIqDpqz3HMmIPpx2QlpPvlFWocPK1rYlYSFzVYrO9OtQbqzoJkDhG4IzjvIJyLdEGVdtH3FhcXMqXyWXQDyCgPGmInlbSHYFO+O4nj65qJjydmQGSbFoa0NtmqJ/heYdUCmZw4cOABPT9FMsBM2bdqUrKiTuASa8eD0R8fl7khuPumkQNHib4qtugXiN5SeJp3lSGW2Kti6YFpVdrpaIqwvzQs0n27FnYA3hTDTGma+aQ6tJa9O12KuCwjrmQw5psVcE040ywkDDGjFWnpQDF0eDkJzKMRGs5FpVRUvcuLECXh5iaZDOiE+C3rhwoXImDGjvmabMO5fzia0WZsrVBj26QY+nDgUnYYWk2pNP5e0VMk2LdDRn0CvCEE1x08IJkPGftmmjTDMzJjiaPmkmbc5vxDlPA5asnDG9nbap4k1ozBIi+1aPHIpYUEzBMkaMIRt6w3gj12aq4SJXxhqqBKXx88nn3yCDz/8UC6caNXWiYx8CtPLL+lrSYP5oOOjXr16sQ5isbXWBvt2GIdMseacoEfS4LDs+DjjDQwWRmBisDmBZgA53RDMDz05mj+XAkwrlvuuiCbFOGFxVlijWaIcHk1+WPG8P6izEG6mFKU4MgSO0RgMb+NchpZ0TUSHM3X3PASUcdGSAW0S1kQ6MiAsCieMZZOey+TJk/WttsvwkSOwuMFInD17Vt9iPfLnz/9Cnmz6oHnPbBlamGwxcpq73uJ3YowpUDyPTQj01DPaCCfCkXYMURtwRJtk1RyGsnF0HmfrJuyUoGiTt2ZpFjdn/OYf3CBCbOP72NyyliDTZcL0pXW2aOFtzImg5mCzHBEREfj0fyZkzfpSsuOLrcHDhw/Ro0cP9O7bB7379UHhr/IJ6+Eq8vyYFz379ELffv3QtWtX/eiEke9HcY4kcOHCBflqb8mS6EKk/5oDp5jZj5FKChsQ6BPC0mT+CcMCJj+t05IjcaZv+nEM3EUTgSFvY4QY0iXBcDUjjwVdHCf1fB3WjFnkUG4+ONgRQlcFQ25sJag9LXH48GE5enDNmo1YsnQVFs4zYa2LCfPnL5fbNm7cJDsO44JiHh4ejpCQENy/fx8XL16U00jt379f5l9mR9qqVauwbNmy55alS5di+fLlcHZ2ltEYnID10KFD0iJmxx8jKDhgxPxhsW//PjTIX01UzktiuQyMEkI59gru9N2HUgWLwc8/4d38AYEB6FC4KXbtFj+MBMIZz+m3ZiuDA3rsPZsdw1I5NP2P3drvOr1iMy4O+pejp09khx39xQZ0EXylDwRhiA/F0po+XA7yoN+MeSkoyJwBhnkNlKvC+nAG78qVy2LPThPCQ0Q1jRRLhCgHm3Bwr+buaNiwoVyqVq2K+vXro2XLlmjfvj36CYt1xowZMgPezp07cerUKdnBSHGltcvoB7oFgoKCnglt9IVWO0WPx/BYb29vmVvj6tWrOHfuHPbs2QMXFxfMnDkTffv2xd9//43ff/8db7+ZUQizl1guI2ykO0q9VRozv56BWflmwuHnFdg7aA8urr0A36vP9wafOXsGZ8+dxRmxNGjaSDQFbyLv97nlOhc+HPiwiYn//vvvmQuIy4ABA+S1pRVocPU/qgk2U60mNWWtPWIzAk1f8nZ9JO/aK1oYHCMbkjvcOaFwHrTV4nPZiceKQP/x4XtKjK0NhZCiyThniiqFjvPy/fzzz1J8u3XvjS6dowR66CCTsJzFr9UGodiP+Ok/jK3WHYUKFMTBdiuQ95PvMOOb6ZiYeQImfTkRk7NNwuSskzApy0RM/GKCLC+tuASNv2yEZnlrwHfAUQQOcZMWePjwc/AfcBxDKnRAmz/+kL7l6HB05WefffacQHP9vy7/6UekPTijDoejNxILXZcppRGpgc0INIc+M9F7SkDfNeeiY+cdQ2AoxnS1MOOVwvIwbpdDtUePHo3WrVujSpUqUnw7deqEJUuWSL+pr2/M8YWOjs4I8DOhYwcT2rYx4YmvCbNmLdT32had/+uM8qXLIUAfROJ+3gOffPgR7t7X4jWDfYNx9+RdHJ18BGtarsHcQnMw4bPxUqynZJssxHsysr+WHWFCmDH6orTCP33jE+wcsxO39t/E49uP5XligmF35iJdLVcZfU/ahtEhTLnA37EtJz1KKjYj0NaAD9Yb/trwbHbeGWLMpPIqvM2y0A1w7Ngx2eT/7bffpAXcpEkTmfTnyJEjcY58i4tPPsmEBvXr6mvCcmrSCJkyvauv2RZ0jcRETJavOWGBYbh54CYODj+AHO99hUAh0DW/LY+bffbh51zlMS37VEz+UljdmYXV/fkETMk+GbPyzsSq+iuxq89OnHA6gaP7j+LY8ePI/GUW1P6+Iq5034Hps2bg+MkTOOl2Urp50gN0Qf6rD0dnlkl7HyyTpgSa+Sk4kwJnmGCAOBO8XBVGh7Vim1MSfg/myd4vWhmGKyg1oDXM3My0fitUqCBFePjw4Th69Kj001oaY7QcU24axGZtpzYU6JdeNclOyaTg99gP37yTGaPGjJLr69avQ4HPv8P07tOxu/8uODV0klY3XSMTPtcsb7pIxmcdh29fzwHHZuPxeNAJRI4UyjTqonSX3Om9F99/+o0c6JPeYBDBrttAoy2aS2SP/aQTf4bdCTT9TUzSwpFJzLTFJyVD9BjtcSsNDIl+EKyNfqSfzZy3Z2nhiIR5nJ2snJaCfmF2hLHDrW7duqhRowZGjRolreGAgJQNW2nQoBby58+mr9kuBYr+gL6XTXDdsVPfkjh4z2NKJ3r+vBDcaDwVP4Sgh4G4c+w2ziw5gy3tt2B82fEo/3URYLSn9GGf7LgaH4gWCB+gbm5uSX5wpBXo2mTOEObPYIe/PaRQsGmBZqjd9ptAj0Na2r9mQog5ZJLJxu3ZRWHe4mXS8P/N057yhGGDrEhMwGQk0O8lvv8i8RtlQifCEZQvmU2TlRxo9Xl4eGDixImoXbu27KAbMWKEzCec0kIcHXf3C/jpp9dFyYRmzV6cl8+W6NK5O4bcNWFipAlNmzXVtyaNfPkL6aXE4e3rjWWNxmBdi+n4rXA9KdTt/v5L7qP4c9qwVq1aoXz58hg4cKCMRknPMAd0+73aVG6cXzO2GeVTE5sRaNdbQOcDmnXI4aAc+ME8Gb527kMizOnBnM+c0ooZ8r5dBpTksPJI8QfQh5sbcNg6h6u/N1trLTCkiPmjm24Vx07TRk+SN4VFbUyvlVDoLqBVzEETNWvWxK+//io76Wwxz3L79v/CyVFUz6cmBPubxENDCI6NcvDAYTRfbsL4MBMmiZ9U1gJ8qCSNKz5nsfJXE+rWq69vSThNf2mGcnlLwOuKF0aMHo2XM7yC9157O1YfOEMG+WBmmCL7DbZt2/bCqMT0Ag2+DeJnwIkzmonfIIMWLJHsKLnYjECnhVAZijAtXcIh60y+RD4SFjKnyHpr5vODaFgBOOqR6UyZsOmxsIyZp4ApTffe1twaPJ7JwynmPI8xU3G2xXE/8f38/KSv+I8//hBW6E/o3r079u3bl+pWcXzcv/8QJYpnQnCQqJrh2nLdy4QtW7vrR9gWjJXO1+glTIjQBJpL5X6mJHeKTl45GLcGm3BzkAn//Ju4UDnzWVSGLFyI9t4++KRQYdxM4Ew0vGbOpdimTRtUrlwZ48ePt6t5IC0JOxc5WTIHo9HK5riL1MBmBNre+Wu3NuMKhZOpBud5iJs7WQiq+J1m0JM8mSZp7g0OOWcifyZxMmDnH/OIMEdICSctHjuf2X5CkTcoskovCNh85ag4hrBVq1YNPXv2lJayrYtxdMaNm4IxI1klo8SZCwer3L6tz55gY3xf+AtMEddriDOXgbdM2LBho35E4mjWsTYwTXzvySYc+0+cb2K0JlYCWbV/P/64eh3dRLnkmLGYMSVpPjFGf3AYO/sgmMDJniZNsCScJ5T+awYgcPo6IyOmteGvQWEBmAuEUKQzTNOme2duaeYVeVUfxl5L/GaZb4BwYAzdG3xS51wqjhPv3yaOJ8wtG9tsFU+ePJFDkFv91lpaxr169ZJDnjngw94JCvoXY8aYUL+uqJZPxSKsUi7TppjEw+aqfpTtsP/AfmQrY0LRViYMEqJMcR4XapKCXb9B0lwyeYp/+Uygubj8bsLqtev1vQnn6MWLaLzvALqIllcXYRT8cf0mSsWTwjQhsL+iT58+z/zY9jRPpCWhYHOkM6eXY+jupdhD1JOFqAUKuibiyqfBbHmEQfGFheVKH/HmaHpBK9nIyMXAeVrLDIujJU1r2YBPX+YTqboOuBjPU5hizCYnhxDTgunfv7/MUcFh0GmVmze3YuokVksT/mxrgqeHCe3/4rrt+UbvRp7FoogqaLvlI/S7YsLoABN++MWEEt1N+LZc0nI15//+VUA8kAyBZnlaAxOOHE1cnsrzN2+ihsNKTaD1hemavv25psxJYil4rsGDB6N69epyiLk9zRtpSbyEQHNy5hrCCOO0YJzP0RJeW9b8dA1jp4sK0TVC9DjDijGhK7dReGn10qLNIoSZIw6nnRE3bqJ2jAEHwRhhcCT7kqg/0OoE5pk/efKk9BWXKVNG+gE3b94c7yCHtEbevJ+Kf03Yv9uEffsyiHtiQqFCrKZCYWyUP1r/JTsH/xHXvPRCJxyPnIvVwX/qexNOOILxZzHxXWlBT9XEebWwoGv9YELJn3LrRyWMewEBKDNufJQ4i2rUePce/K9oUYwSD31rwZwhzIfCOsxBS7HlD0nrMDn/tHNAFWGINd6mhQUnhTQr0Ex0FNfQbXZKbhOtM0ZTsDOOccUH7mh5o6sJseXcgvU2Aa5mLbjvlgNjT2o+ZDZxzGGHnzE3YUJgU5HhbIwxZpIfZlBjxrX0zKjRE3HnJqukCeXKsaPNXfzAAxAW1lc7wEb5vvBnmPjUhOLtTLgdnvQRexeun0H5bCaUKmlCvXyaUP+U2wTHiPrwCBdt6UTAiOcfO3fBf+GRqLdhk/RF52zSFPTEPUwhdxiNCyarYoRIgwYNZOZAdqqmR+j6dLkCtNyhRYowXPhGAuKw05xAM48srV4m6l8jLFdGPxiDPjj9ztF7WqA6k/4zjI9k1CeJ9WA60wWAsxBrpjNdf1ULiTv7CPjNVRNmds7lENsWeGjvic6UGCaN5Qi7OXPmSDFmU3DKlCkWn5Lf3gkMDMK//4jqKISuWRMTgoJa6Htsnx9/MWGy+Cl9WcIkWk2ikiQR9wgXYYlngyv64Nt6mkDvam/C1atJqyuvZsqEopMmoeDw4ejg7Sss6aeoX6uWvjd1WLlypezIZogno4rSM2eF3nAyaE66+1ssY5vsUqDZ6uc8gzHBuGGmLqUPiNBB8NI0rUzh5ROMwtvGLNUuO/joZ14ntud1AOoIyzmLEHAOlGEOagax00+dEPx8fbVOvFatZD4K+uU4ICC2PA0KjeLF80pxvnrJhHnzMthNp+ftW7fRdrM2QKVg/Y/0rcmn6/7c8OgpBH+KCX+0Tby7hD+SkaLOeYaF4ai4lx8XKgwGKlaYORv37uiWSSpDw4W5WijY7OxOT3NOJhS7Emi6HCiaJNNcbRQek/o7XtK2GbDDr8sBLZqCVvJH8zXrlyP0mMaUQemMSTbgjCtGFixa3AmFQ2eZpa1z586yknXs2FGGtykSBxPwnz7JqmhCgQJ81afXsQMmjpuGkY9NGHTThAGr6+hbk8/xiHlorLs5SuR4U9+aRIRYt96/H41375Wujlz582vbbQx3d3f89ddf0rDhxAlpuTM8odiEQHPAhWssrTjGEXO49/DjwDtzgO+XA7tvAc3Fb5jNA2LMqmJAfzAt5+lngdauWmpRWtGcLotB59x3JAnuXuah6N27t0yX2bZtWzm1vnkSH0XSqFZVVENhPQ/sb8L9+yX0rfZBlZ8qyrC6xrNNOPJIVE4LEfo0AF+V1wR6VUsT7txNXv/EHWFJf1S0qBToX8+cw9rVq7UdNgp91Zx0gG5BxvczGVd6JFUFmukA3xSWbM2NwAJ9BB475zjYg5YxXRmMnOgvLFx26p16CJTW6xWHT5fVy2VdgGO6S4MwEoO+4kGJnEHXgM1rJqjhMFjmpmAHB4dEc0CIwrLUqVNfivNjbxN69MiAyEg7yGBjRq6yGWUH4Xc1TPAL18N/LES7DV/i3mATwiaY0LN3f31r0hnr7Y0SgwZLkc5eqbLsxLMXOJsN3YUcls4+nPTyW0xVgeYwZg5f5lBmTrRKKMRDhbDSL0zR7ifEmZawsY+DO9gbyh5QjtQjW64BO5LR58aIijFjxsgOvMaNG2P27NmyQiisC5MhrVzBKmhC4UJM02nmd7IDGEJWRQgoOwizlcqgb7UcOwNGoVNpzYou8FXyc2CHCUHO+Wc7dA6LwL+BQejYvr2+x77gg4VzSzL6qVatWnLuyrRKqgo0eXW6qH9CgC/pc2pytB3ztnJh9jZuZ3ibAfMi7xSGCnO9JhamcmRgPeMzaRXT1zV9+vR0O3w1tSlS+H3xr2jCO5hw+nQO2WKyJ04cc0NPdxPGBptQu+t3+lbL4R9xD1/TJy8Eelo9jqZMWn4PczaK30DWqtXkoJVCvfqkCRcdvwN/08wfQhfkpUvROqXsmFQXaA4SoY+ZLov+RzTfcJYFQPs9gIOnZjUnZQp2TvZ58OBBOaEnE8sbmdtu3bJsM1SRNHr0EOLgYxKibEKdOqIZH2Z/Q4b/+ftfObz7vyMmLDpBx4Hlabzof/AdYULoOBMmTNbDkZIBrc+aDg5ofcFTujqKlSql7UhDcDQj89GUK1cOs2bNsuuHUKoL9JIL2oSxHBLtmcSJMh48eICtW7fKCUc5JLpdu3Yy963yGdsm3t4+GNBPVD0hzj/XYBW0zwlOC5TMJd0b5buZcClot77Vsqzz7oZh1TQrusgPWfWtycMjJAQfFSwkw+7qbd2OE8ePazvSIOxPYmc++5JopNFos6e8Naku0ImBuSkOHTr0bOw/3RQjR46U0/mokBz7oVChr6Q4nzlpwurV7yDcTucky9/oZdlB+GVxE4LCrNO5+SD0Er7OJX6m003oXZEDYSxDz/MeqLZwsXR1ZCtcRNuYDqDRxk7GSpUqydw2tt6itkmBZppMpjnkjeScd7SK6VtiQnFaywr7ZeHCJbh0ntXOhOLF6OI4pO2wMx7cf4DmDlrmutzV39G3Wp6nwtirOvptBI0zwXeUCUuXr9L3JA9vYdB8WbOWzNHR7s49TJ4wQd+TvmD+mw4dOsjZhObPn/9sDkxbwWYE+pdffpE9shxRxAxunJxUkbYIDQ1Ds6YvAZEm/NfJBH//n/Q99oez0xoMu2/C8EcmtJ9SSd9qHZbca40FjcVPdZoJJYslbTqsmFgkxCh369ZalrumzfA0nY92pX+eA8+aNWsm46+ZrCy13SE2aUEr0iblypeS4vzgjgkjhr+CyEj7TZxTrXpVTHpqQquVJuy4OV3fah3uhp9FnpzipzrdhNYys59lYJhgsREj0OGRN7oIIWpQz3anFUsN2LnIJGa0rpnyl+7VlI4dVwKtSBEOHDiMvbtY3UzI/6NJWNNLtR12yrdF35f+57wNxQMn8oK+1UoITSjeVcsTfamvCa679FkfLMBJsXxSuIiM6Cg/Yybu2kieDluE7g+6XTlZAVOqpsSku0qgFSlC6VJCYER1mznVhCtX8gtLRNtuj3AYMiM3KNCZi7yEiBTo5JxxtybWt9asaM6kY0la7duHxrv2aHk6ChbUNirihfM1MtkTJ2BmDpFjx5I4dDkOlEArrE7Llm0RGW5CcKBoorcWghZh3x29J0+4ofMRTaDL//mFvtW63MJBlPxW/FzFA65B3pf1rZaBwagfFyuu5elw98D6tYnLPa3QYHa+CRMmyAEzdInQn53cLJZKoBVWhaM3f67OamZCyRImhIaM0HbYMYMHDpEDVPp6CpF2batvtT45fxH3cZoJR7uYcPGSZVNzTnz4ECUHDZEinbVCRW2jIlnQh+3o6IjmzZujfv36WLRoUaKjRJRAK6xKaOhFYTGbhBVtwokTXwiLQt9hx7TtXQ85q5nw+Y8mnH2ccnkgRnuUx/4O4ic73YSGjRrrWy1DqPjDfP/nn+gUFIL/IiLxT/u/9T0KS7J79245nR3TEzP5E8OJ47KylUArrE5AwG0h0jXEkjZynmwI7oSReBcDxc/ncbC3vtX6XIzciJ9/ED/ZqSZU/O4Nfavl2Boejo8LFsQX5cvjbyEkCuvDae6YnI1hfTGhBFqhSCop3Rp4+hTZa7wk3Ryb/zTh1m3LZlxkHHQX8fqPWJzCwuTnKVIXJdBpCMa1prclvdFtx4/w6mtCxCQT/mwXvxsiMvJpjPcttiUwOBjhoaGICI+IcX9qLukRJdBphCtXr6Fe0U/RvW6udLP0rP8dvsmeRb8DFKNImb1w4IABdr/069c3xjwRJ54uwG+FNTdH4RxM1xo32T59Fz3qfRfj/bOnpZf4W/+Yv4D+rdIPSqDTCBTofk3yYmWvCs+WFd0qycWxR8Wo9a6V4NC90rNjuI/bzbfxmGdlsY+vDvrrc9vEe+Q5ud5T22csjj3FecV5zJeV3KYfb/55XF5YN66L5xbrxjXxvMY25z4VUSDPt/od0GYG79kgD5zE9uiLS89KcO4dtb66VyWsEduMhfvM11dHW+di/n6WeYxRNt/nIs7NzzPW5Taxzu3RPyf6eY1lYefScF7ton+zKAJDnuAbPYn/iuYm3H8Qd8bGwrm+gJM4v3FfB87ujGabZ+O39VMwf3AdrOpZHq3WTcWyfj+JcjlMHNcSv2yajX+XD4Fjr4roP/s/jJrcVr6X+3ot6Ik2LhPReNt8cZ458rX12snyPDyG5/hr1Si5zqXLkgFY1as8nHqUw8BZndB0yzyMnPInnMRxxv7mG2di9rD68jzm522zZtKz867uWxFFihbTv1X6QQl0GsFcoCm6nvu+QJDP63h85y3cPP0RVvYuL44ywffG2wgPzICtE4vIYx/fyQi/WxkR+vhVHFuZSwolj3PoLoRQLIgwwalvOXGu17B5fFEpkCyvHVIK3tfewZN7byLw0eu4fPAL8blRArt9SmH43nwbEUEvI/DhG+Iz3saW8cyaJq5BbA8PyIA1Q0rLY9cMLi3O8dqzB4lTv/+zdxbwVRxdFH/Q0paWunw1XArF3V2Ku5WWooXSlgLFHYq7u7uT4O7u7u4kEAiWhJBwvntm38IjTSgSYtw/vyHvzc7O6ps9c/fOndzwlW3clHVuX33XNNRcb4Y8BM5s/xInNnxrHgjBNdDNy6V4tA92miP1fnUpJsZ1tLbH9PPChPjI6y185vkOPpP947JYt2OY75/K99/kXHwqx8UyH7Kc5PUYmPHR+kO6Z8Uv8xOZz39O+x69neez05AM+N+VmPhc6qk1N4k0TPnRZEJKfOr5Nr64+g4G9sqKT72sepm4rQG9sjyq105jG+YItoEmv85ObGJE+/ZxoGOnLs7c4HFtoNnY5du2CFUXDUOf/jXNj9+tqRz3nVty/CVQZtVkfH9iD0Z0LY9GkztgaptCKL52Bmq59TON7N/SmObauQwTOhTHxPZFzfoT2hfDeFnX3m9ug/nTWxdArwG18eGtG5jbLCd+2OSGQpvdMaZTKaQ8vgtVFw5HjfkDkXvHUgzq9ZMpy3rG/lMKjkCpt0MJjJdk16sNtBKpcW2g145Mgxvn3n+kVPmXjSweiOoSJXpsbRwcWh4fR9fExr5FCU1jx8aRcTLsxtBuoNnAct07HjHN8oXds5nPpoE+/QFWDk5vFO3tK+9iuUsDxsTG/PyeL7BxvLVfC3tkhe/NtzCtcUF4nvwIG8amMmUu7vtcGuP3sFgaKu7HLfm8ZmTaR/vFhv+hfzTsmP0drh79+FFD/jwN9IdeMeTH/7iBrrA0Pmq6JcH8vwvCXfZ/zD858Mm1t7CoYSHMl/1jw+om+TXdE6P8svhwl/M2y6WXUF3y378RA/OaFMRX8hAsuSqONFa58IZPNLMu62SD3Fceag5/hzQ4uTBdHpKsg/VWXBIf1eYlMp9d67XT0xrodfd6o0lu+emKis6S7EtnbvD8u4FeiPQHN6HA1vmIffk03JpkNw20aXAfwjTKM6T88G4VTQPJBjr9oU2ifEcjx+6VpkFlPWx02XjMaZbL+T2XHHduDOlRGTF974mK7olM+9fhDf8AszxawENMa13Q7MeQHj/i45vXMLjnT4geEIBqouCpqLlshiQ20FTc9rlg0gZaidS4NtD7lyTA4dVxTEN2+eCn8PV+y2qgRQ2zcaWKZsN99djHWDsqjVmHJoXA+9EeKe2gDfTda29jaT9RwNJI+3lLw+TSQHM7Vw9/gnWjU+Pc7v/hyuFPMad97mAb6IfSWHH9szu+NMtntc4L/7vRMb9rdtkv66Hy4F50zJXGzv5xsoHmw4XKn/WFRgNdURroj0W1x5GHQb8+WUwDHf2+A3Hl3OTY8T9pMKxtVBOVXHZFPNOIdhuUAf8MSy8NTR7EPxMLCU+/j6HdsuHri+/iS1HNXB7/bCwpK8clqeCmr+UhkBi95by9J8ecZc/nph7WW35ZPPy8QB6Ozv0Jmp7WQHv7XUUCxoiWBnpgGbmmd0KORR2cgv5l4VDEP38MTSe0lnOTyzTQk9oVkcYyUBrqYnJ8hVBYFG+BLfNRYu10VFk8AqO7lMVvs3oZBR20gabpIu7lUyi2fhYqLRuLP2Z0w/88L+GLa5eRZd9aeUhVx5v+/pjYrqjZj54Df8U3V86ZRp3rc50Esj9spLWBfhJtoKMIrg30vC45ECiKkw3rVFGDbFRtBU21SxMFG9Zt05LDQxppNnjLBmTEA583RGFb5ee0y41ZbKylUWedbKDdOuY0Kpm3jd1Ar5BGaW6H3GAA/tnS2BpbtLMRCklBs8EN9Itm6ji+/lvT8PrfedNsd17nHLggivrwqrjmobGwRzazf9x31ud9KRa2Tvve1Pe8DfREeWjMlQcTv1NBV5+XGG7ynXlsoNlgU/26ruvaQLOhZSM8TY4zxr1oGCnn+YObMdCnX2ajnEfL8bx19w2jiqm4qaB79c8kijSvUeWZd3+O+lOTm3pfpoFm8KRSwz/GnZ4OePdwYPiocc4F/yZoA00FXMt9gFGzbAjHdSyJd3x8zN/mE1rhbV9fVFwxHonOHUGRDbNNo1uDtuCWedFockdkFxUdtIG293mOKOivrp7HsG6VjEJvOrEN/praCcXXz5TGvQc+87pqGuO37vthQO9f0GZ0U9Pg55F9yrxvnanXNNBSrzbQFtpARxGCviRc0juLKNlP4HniI2yZ+r1Rql5nPjCN3FxpqGg/5udtM5MZc8jJTd+aRpzrslG8evQTeBz/WBpuaWCk0bp44LNHqnbDuFTGbnxq89dGjdMuzIbV3radaDNmQ7t6eDrzfX6X7Lh86FNTH/eP6p77xAcB92Xz5BQ4stpqmPcuTGTqPiH7xQb/+ukPTR0sy/2dKw+Q52mgaQP+RB4ytDHn3foVKi+Oj1jeb5rvn3u8I935XPhUlgdtoKvPS4Ryy60G2s4bJcf6maxDM0ZcUcw0cyQQRT2kezb8Ouc7Y7P+8EYMaYATSUOWH0lOfGC2Hff8e5jiPMcVlsZD1fkv2EAL7ldaoF8p+fmKis7w/WNPlqAEfUnIhnhSe0vJ0pZMm+/IruWNWcMuM6JrBVOGjSTNHHb5yW0Lm/X5eZYkmkFmSsNtr2etW978ndbGMmfwQTC6c1nT+PJFJOu2zRmsn8tYp2uDPLxbhUef7aQNtBKpYQPdoUpq02g9TqIWTXL5Ljf642Wun12/B8kz6wRdbue5lAuagl1Pvj+xD67fn7acn+Wvy+d57Qo8UwPNNEcaSjaWTGywacKwvzPZZYKux3K2ucM1sY6gf+1GnJ/tfCZ7W671hFSvnf6rgfYKOIVkDJ4kDXTTvJx019+55EmCNtCRNWkDrURqOBVY5rTJkS9butcm5c+eDsWKFnWegac30JEt/VcDzamwCnZ7D359HLje1YGZs4MvazfQNEVQudomCVvFUtkyueaZz05Fay2nS5ydHpe3l9ufH+flMXXRDGLn0d7MfP59XM5al6aRoHnWdh5vUxtoRYnk2A00u9/9+mQ25obRnXKi+bhU0m3ObkwlHYankx98fmPrrDM7qWkMJrbLLV3tHNKFz4Ma7olRe+53qC3r1nBLjOFds5vvVMdcr97MpJja5nGjNLR7NqnnOzSY8r104a1Gjeq5/Yi0xlWPdTKP9uuugzMYM8gk2R7zRnbJjraj0uDP6cmMRwnr4d/f5fu4Bk9voMlUj18x42dLRWfPlNqZ+yRsoN2kkfvq6gVk3r8e7967a3lReF83jWXZVRPRekwz03DTi4NmCL4wjBYQCPcm2fHDZnfk3rnMLMu3fbHxoY534Th6DqhtjqHglvloNKWj+cw0WdZno5J9z2rzd3DPKnINyiDag0Dk3L0CjoCH6DSsvpyHH/HpTU/T+PLl5GTZJveH6/QYVAd5dyzGe3dvI+3hrcizaylmtftBG2hFiczYDTRf5H1z8V0M6plVGs7kaDsiDTLs+wzuTQual3mjOmeXxjI9kpz8wDSmmfd8jmTHPzINzAhpkH9clACFNnxjPtM1zsGXrE6zxVv3ohuXObtB+kvqz7rrC+MjTXc62rLjnY1lGlp6h7A8G3G+kCy9Ki5ajkmNGL7RzYvGjvKwyCj7xYfD8G7Z4LjvMPZtvnz8LwVNruEwUju9OczowmBgA+3e3Gp8uwz5A/Ok0aU73Pt3vDGlTSHjwZHw3BEM6PMLvjt9wKjZHLuWI+nJfWg7uolpQOl6x5eHc5vmNMvpAdK3TzVpUHOiyMa5+Htyhyca6Lf8/LCwURbj+1zTfQC+vnrO+DmzLtq03/K7jxFdyuOL65dNXrTAh3jT/4FZn/vJevnASHLmILoNrmfKqIJWlEiO3UBPaJ8bjgcOVJ2fyDSsVL7R/RwYRpe4SzGRf9PXSHPwU+NhQdX7wY0Y+OrSuxjX0Wp4a81JglLSmFKJ0y7NuurNTGbSm77R/tVA59z+P+NuF022wb/RfR3SyOQ3ip0qPt/mr40ytxvoOBfeQwyf6KLm0yLT3s9k//IZTw+ub9uun6WBNlNh/fU2Avo7cLadA6vXrnMueIxt4uDLumyiatkws/46c/qg/IoJ0hivwFce50XxrjQj/NgYx7jvZ/aJCnZOs9xGVbOBts0kbNDTHtmKHHtWyboX/tVAs5GNIY1wxoMbzEAYqvZRncua5TRZsNHhy0K7gX7z/n15GDTG234+RmGzgeZDhA101yG/m/W0gVaUSI6rDZquczXck+AjrxjmMz03vrnwrvGF/kDy3vN+0zSGP4hSLrYmtnF7y7L7C9Mw/auBDnBgTKecJgVV0FToCU7HMu54Y6WBp/mCDa09AKXy4gQouTrO4wZ6bGqzLw0nJzcNv+0b/UINtDDkdBksrWOp6GJFCztzH8MGeo7UTTPG/MZZ8ckNT2PimNrGMkUMl4ay3ajGiP4gwKjjUmummoYz3sUTeEcaTCrfoA00FXTvfjVN4/rDJvdgFfS8JtlMWZYpvGkOCm6eJ+ckB8qsnoKse9fKw7KiSwPtbxryurN7P1LQ2kBbaAOtRBnsBpomgjzSCFabnxhfXo5pGj2aEWLdjGH8nmluKLY2tjEzOKRRZKPZanRq0xBPl7ya0kCXXO3SQD9h4nhSQdeXBprbYll+Z7nUhz4xg12qyXbeEMU9vRX9qROjlNTJbeXZ9pUpV2VRQmR0UdA0cTxvA30Ve5CZM34PdqBsymjO3MeYBrplXlRbMASZDqxHq7HNTaPIRJ9kNsqzm+dCTff+0qDmRra9qzGlXWGT333Qbyi3apLsfwFjh+aLQ65XavVUDO1e2exnvVm90GXoH4/Ox9TWhZBr13LTONt5XK/unN6y/Q0mTgcHx4zpVFoa7rmmvhy7V5gyXMeMKpRtU2mXWzkJA3v/bOrQBlpRIjmuLwkniJod/08u0+DxO9PkdtLAyN+Z0mDOaE1f3bwYJ4raXj5RGt6pbfNIA5UHk9pLI+HMp3K2P49l/BBZ3/7O8q5lmea0yC+NeG5Tt719u05uc6IsY97slvnNNu31WLf9edwzNtC0c6Ss9BYeSgO9rZED+w8ecuZbfB/3cwz+LQsG1c3kTJldkut3+3NIZYIra38OaZ2geSGVc80P/vPQ37MgQwYOknq90AZaiTL4Sdc6daIvkSdt/EifsqWIjWXLlzuP7On0PlQYW6VxppmjfOWfnbkWFy5cwImTpyJ9Oi7p+vXrzqN6fdAGWlEiOcd9V6J0asvMke+7N525SlRAG2hFieQE4gGSFn0DGOaAe01OhXXZuUSJ7GgDrShRgJars+FYa/k5D3SgfgPOLKhEBbSBVpQowB7f6ajDwSpDHMiW9L+nwlIiB9pAK0oU4AH8ED+7/JyHOjC2kgO3bt12LlEiM9pAK0oUofrE703gJI4s7NGrjzNXicxoA60oUYR1twYhb2wHsiVzoG7r8s5cJTKjDbSiRBFu+dxEO/lJ98aXWOff3ZmrRGa0gVaUqESg868SJdAGWlEUJYKiDbSiKEoERRtoRQlDatWqhVxp4iJX6sif/vdJLOdRKa8KbaAVJQwpX7483NoUMEH0QyvNbZ3X+mwm2s1nPs9vk9v8nSd/57XJhTmMwOcsH1op23cfO49KeVVoA60oYQgbaM5IbsdKftm0qG1WePd5z8yxuKdTYuztnEg+5zdDvvk3YEA0HO4SDzf7vI+T3b4Nto4XTVmTaAP9qtEGWlHCkNBuoNkgszHm53v93oZXnw8wvUUBYIDVQD8YEB1zWubBtBYFTblZLf89C/eLJm2gXz3aQCtKGBKaDTQbYKrnHf98h52SLvT4Ag+lYZ4WTAM9vWUBPNQGOtKhDbSihCGh3UAHSAPMv1THC1pnx52+78CtVa4nGuj5kr+rU2Lc7vuuNNShp961gX71aAOtKGFIaDbQc1rlwb4uCU1DvKlDSvN3Y4dUWNI2Mw51iS/f82F/lwQ43DUu1nZIa5YHV8+LJm2gXz3aQCtKGBLaNujwTNpAv3q0gVaUMMS1gZ7eIr9J1ucCjxo+W+nyr/3ZNk3wL8u6JiplV9OFXafrd6tc0Pwn8/jd/A2mLntbduI2tYF+9WgDrShhiN1Ar2qXAXf7vo17/Wgzzgnffm+ZF3ic0ftkt29Mw3mgSwLs7pTYNJjXe3+AGdJYnpBlXMevfwzjtXGnb0ysbp8Op7p/bRrSBW2yS9kPHzW8XPdGn/fNOrf6vIdlbTM5646Pu5J3W9ZfKnlsdH2kPu4DtzW7VV5TjnUtbpPFLGPy7f+W2e6a9mm1gQ4DtIFWlDCEDfTs1gVwr+87puGzG9KLPT8zjd72f5KZF35TWxR0emDkxsI22eTzG9jRKakpP7V5ATwcEA2zpBGlwl3XITXO9fifaWTnt85hXga6NtB+/d/EbKlngdTjIw+CDR1S4Wqvj423BxtkDLI8PwJle/x+V/bNfvnIutzlAcLtbP8nKY51i20+q4IOG7SBVpQwxFbQbHTZWHpKQ8mGlN89e39kFDFV8tr2aSyvC2k4rzlVbKA0ynSXYwPJBpovCbkuG2g2qL6ibP1E4d7qy4ErjxtoqvMrvT41CnhXpyQ41/1/2NoxubVc6vLv/wbmtsr1qIGmQubD4L407FTYbKBZlu58x10Gu2gD/erRBlpRwhBXGzRVMj0smExD2j+GNKSfiNrNY1T0Bml4jcucfPbq/YFplKl+g2ugz/X4wuTPb5M9WAU9UxpeqmTm7ZRG+nyPzx99Z/2uCpoNtHvrnNjTKZFR19pAhx/aQCtKGGKZOPLjTI8vjUK90+9d0wizwdsrDeLStplN43qjTyzTaHLwCe3Q/Dzfaepgw04/Z9cG+oI0uPxMJU4V7tpA33cqZH63E8tz+1TXy9tlNErdmE2kgaayn9c6h6njRNdvzGeuwwb6hDbQYYo20IoShpQrVw7ubQuYRnpWK/4tYBQ1kxXsyP5s5bsuZ+I6rn/t9GQ9QdYJ8p0puO0/qvuJup5cx7V8Nm2gXznaQCtKGDJv3jw0a9YsaqTmzZ1HpbwqtIFWFEWJoGgDrSiKEkHRBlpRFCWCog20oiiKoiiKojwHKqAVRVEURVEU5TmIMgL63r17OHHiBG7cuOHMeRIfHx8cOHAAN2/edOa8GLdv38bx48dx584dZ86rwcvLC/v374evr68zR3kW/Pz8cPDgQVy/ft2Z8+zcv38fu3fvxubNm3Ht2jV4eHjg1KlTCAwMdJYImStXruDIkSPw9/d35iiKoiiKElUJFwFNofu///0PP/74oxEtz8vUqVOROnVqbNmyxZkD9OnTBx9//DEWLlzozHmSM2fOoFu3btixY4cz58Vo0qQJvv32W2zfvt2Z82rgsXXv3h3nz5935jwfAQEBzk/Pxt69e801yZ49Ozw9PZ25MIIyduzYSJQoEerUqYO6devi119/RZs2bUxn4uLFi8idOzc+/PBDlC5dGlWrVkXixInN9+HDh5s6RowYgbfffhvjx483312hQI0bNy7Kli1rOkE2vDd4PU+fPo1169aZc548eXL88ssvyJs3Lzp16hSssKXo7dGjh1nneZg5cyY++ugjMzxu48aN5h7NnDmz2dazdGKWLFmCAQMGGOH9IjyLSFcURVEUJWIQLgL65MmTRhBRDNFiR8HjcDjw1VdfIV26dPjss8+MqFq+fLlzjcds3boVCRMmxJtvvonvv/8ehQsXxqVLlzB48GC88cYb+PTTT00dn3/+uUmMe3Ds2DFkyJDBbINijuWzZctmylIkcdmGDRucW3jMgwcP0LlzZyMG48WLh/Tp0+ODDz5A/PjxjXWY22SdMWPGRIoUKfD777/j3Llz+O2335AmTRpT/v3330e1atWMOOzQoQPee+89rF271ggmCtG0adMacU+LdokSJZAzZ06MHTsWceLEwSeffGKsoRS0rIvHnDRpUrMtCtIqVaoYi/qECRPw9ddfG+HKY3/rrbfMublw4YLzSJ7O0aNHTZ2tW7c2wrVIkSK4deuWWbZnzx5zvN99990jAT1y5Ehzbq5evWrOHxPPqSsU2O+++y4WL16MiRMnIlasWOZvUCiQKc4rVqz4hICmEKeg57nhuWaHideAnaCzZ886Sz0Jz32BAgXMNenSpQu8vb1RvHhxc80yZsxozqGbm5uz9GN4PDx/vH+4HZ5/CmHeIwULFjRW7Z49exqBPX/+fLPOpk2b8MUXX+Dvv//GqFGjjNjnfcl7bcWKFaYsE+vj+eM9wk4ej/Gvv/4y9xTvEZ5X7m+tWrXMOVUURVEUJeITYQQ0xSJFCaFVklbPevXqme9BYXmKbFcLdL9+/UzeokWLzHdabikKf/rpJ/Od+RRSQ4cONd/pztGoUSMjngsVKoQ1a9bg4cOHZpnNtGnTzDqs26ZFixZG3O/bt88IaIpECmKbnTt3GtFGsffNN98YAf3ll1+aY6No5jYpgsuUKYNixYoZoUmhxu8Uv7YQ7dix46NjpICmEKOV1rZU9urVy+wb63V3dzeCO1myZEYo8lzy3N69e9eUfRoUqBTxFN08FylTpjSCrlKlSsbthcfJ461du7ZzjcdQvPPcJUmSxLhN2HA9int2UHbt2mUEPgX05MmTnSUeQwFN4clj43o23D4FKu8FV3jv5M+f33SOKO6DwvNFMfvPP/+Y71y/ZcuWyJo1q7GUU0AHZ51v166dEby8LwjPOdehIKeAJrzveC1paea5rlGjxqM3KNWrVzcdAbr3rFq1yhw7yxFeB94TPM8U5rzm3BYFPa3qPBbeS4qiKIqiRA7CRUBTZFDkUSRRQNPK+84772D16tVmOX1JKUBolQsOvp6n8KDQ43oUxxS5FLNz5841ZSicEiRIgAoVKpjvFJm0MFKo0LpKd4Po0aMbqy6tj7RCBhVWtAjSkkmBw22x/mjRohkRRZcHbpP5rpbyWbNmmc6BXS/FMY/VFu6sk+KSgtG28tLVgcLVFm+Eoo/bo0CmWwJFKq3ttmDjOeM2aKHmNinIuC8xYsQwwpvHx04EBTnFN8Xotm3bzLo2XMZOBsUgXTFs6J5CwUurMLfPjgDrdk2sk/7mFL2NGzc254TnhueU144CnuKY0OofdH2mBg0amOULFiwwx899Zx0U8zxvdIsgvC8osrkOj5nnlyLU1WJts379emOdb9++vTlXvIe4Hq89zwEt2MG5DdF1g9ulywqhe0rJkiVN5+HQoUMmj/C8sz6G3HftoFSuXNlcb1rzeT/Q4kzBTdjRoOjneeY5a9iw4aN94r6y89O2bdtn6vAoiqIoihL+RJlBhK8z7EDQjSJTpkzGykoLN90D6PpA8UcxTQGvLgIvzuHDh407h/3mJKTBqv8FO2l0B6GLTY4cOYzPOd+28E3Jiwx8VBRFURQl7FEBrSiKoiiKoijPgQroINCHOV++fMYNgoP6GJ4srOErf1qP7VB5jALxxx9/IE+ePP8arPcqYKQRuozY7gwRDbrn0D+evsYvw5QpU4xbBQf9vQx0c6H/M9196KNOn2la/jnIUlEURVGUqEe4C2i+Cmd4M/r8cuAX/Ufpo0r/Xfqr2oMC6X7AiBr0MSUUKfQd5rr8zCgaHHjHQX6MokDhy3W4fODAgY/EKH126ZPL5OpDS/9T+kfTj5Wv1FkX94H+2hxgNnr0aOP/ynz69lIo0f+Y+9iqVSsTYcIWTIx+0b9/f5NHUUX/Voo1+mdzfSb66gYXM5h+yvQvZrQODkyjnzWPpXz58mZgYu/evY3/Lweo8VzYAx95rAy/xv1hNA0ed3AC7vLly2YA4vTp0x+5dDByBMPCcSAlE4+H27XXp4BftmyZiSLCczFnzhzjv83l3B8eF/eD7gmMusGBh4TXkftB/3IeK883wwyyDvoo0/fZ9vtduXKluf48zzxfvGbBhYRj/YxgwevHazBp0iQT3cJ2f+B+DRo0CGPGjDHHx/uL557H1LVrV3N8tg80rzfrYp3EvqYMH8jyHPzI82XDgYU8b9w/XoPZs2cbMc9zwDzbX53Xir7cHDjIfA4y5XWxt0MYJo/n3Pb7VxRFURQl8hDuApqiiqKZA+EoMmj55QA7CjKGB2MoMw4mo+ijqKRllAP4KHA4kNAe4EXRRkFD0UMLMgf+MeYzxSz9gSlqODCMA944aIuWZle4PQoklmUoOQohCkKKdoohRqGgYKQAp2ji4LssWbKY7VOkUXRxEBr3mdEhGJKPYeooAnlsjMbBMHAUeow5zMFwFFBBYf20rtLXlmKaApOJg9Y4oI0imZOsUJhzv1g3Bx9yGc8H/WspWDlAkwPVKC6Dwjo46I/7zHPJwZYMx8ZzQHHJ/eb2eWwUfYz2wXNCYUpfap5fDoBj54bnh4MkuR/s0LAshT6FKPeFddOaPmPGDHN+GLVj2LBhGDJkiDl/HHTIzgTFLQeE2mI4uIF+FMccjMfrZ0fg4DXLlSuXCb3HDk+pUqWMbzGFrz3Q8ueffzbnxN4frs/7gvtBAc37j+uy40I/cp5PnmOW50BOinkKYQ6s5H7zmvJNAOug6F66dKkZoMgOAL+zA8d7lZ0H3nO8jxjRhWUo7Hkf8f4JGnlEURRFUZTIQbgKaAqJVKlSmdfftNZS5FDYcfIK22JMoUiRRVFEsUSrJUWNHQmD0BpIsci/FHV0vWAZ+9U84wYzhJgdUi6kV/8Uqgzlxu3b1mkKREaHcI1hTOHEKBHfffed2QYHmNWsWdNEXqCI537Rkk2RTxi7muKJIoxQvFNo0gobFIotinwup+WUHQMKdgpoii47WgajinB7tMBS6DLWMAUpLawsY/8NCUbaoJikEGbHxbZkE7qL2AKalmeKTA5EpEsHw97RokqBaUNrOIUqw7IxFjMFMUPJMRqHHeKPllvuLyOQsF67HsZqJrRK252ekKBFmQP4eA1dQxiyA8OIGbwHKKDtOtlBoWjndWD4O0Z3cbX8s0PAe4LHyHuRQpwdNH7nNWWnifcRw+/ZkWL4hoP18BrTeszrxagw3Cc7dB6PlWX5JoCdB1r47XyKcKYffvjB3M+KoiiKokQ+wt0CTbFDiyitzLT80T2CIseOckCxQxFJS54NBSWFmg3LUPBQ+NCVg8KRFlAKF1oEKYxpTaRwofU3JCiG+BqegpefCYUVLYzB+R5zHyjGuZwWUXvGOh4T823hRJ9muijQHYTQkkqrp/09KBSKFF60/vJccH2KV362t0ELOY+XYp5QANsxiHkuKepc3Q+Cg8t53oJCgUtxaJ9z7g/jPHOfWTfPkWvECC7nteN+2vDc2GHsbGhV5rXk+WI9PM+22OW+8xzZof1CgqKTHRxa6bldG3Z4KGqDzhrIY2Bngdvj+WJcatvqy2U8Tq5ndyC438wLek1J0Lp4LLz32JngeadbBmFd7CCwDBPPM8uxblrgGYEjPHzrFUVRFEUJHaL8IEKKFroFUDi7CjwlcsPOCa3KkQW+EaCvNDt2rsJfURRFUZTIR5QX0OGBbTUPacrpZ4GWT1pLaQEPTWiR5+BDClBXt42whsdFS7c9y19owrcHtABTYPMY6Q5Et5mIHGeZVmzXtyyKoiiKokRcIrWApjii3yn9kW13iYgAhRAHE9LlgYL1afAY6OfNiVDoW2vDgWr0LabF8kWgiAxOINONggP6mJ5FvNIVhC4HHJz5IrAzUb9+fTPw0Pb5pQsFfZXp0/1fbiYvAl146J/OyUm4fX5nVJTgpv7+L3j9/usahgY8D5wEh/7nr6JToSiKoihK6BEmAppijgPV6IPMEGiEA+QYqcCOasDBYQwfx5nZOBiOUSz++usv49tKn1MO7uLAPApNfqZwpghkHgenMXrGb7/9ZnxoObCOg7o4SC5jxowmSgSjN9AizLo44I2D5xi1gtEqgvNFpsDjoDRGZmAdHBTHmMH0seb+MsQcp8/m4ETmczn3ib6tjPrAdRl1g6/r//zzT/Od01Hz2Di4jtvmgDmGgONU2TwGbovHQKFXrFgxs449MI0DC/mdx8RzwGgl/MxIHfRPZh7r4fnjXw68tKc1t6GYtKes5vmgkGVUDdbLdVgHzyfT/PnzjX81B9axrsSJExuBRx9gngNOvc1rxHX4l7MfMj8orJ/nhteegww5CI/+7TzvjCLCepnPwXw8l7wWFPm///67GcjI88Vj4j7xHgnOd5gdD/pF83qwLg5M5T4zmgjPDTtYPEZG0yC8b3i/8Nh4z/G60A+aPtv2vcd1uIxTbXMQIX3SeR+xHopzDlqkVZvRQ9KlS2cGuXIQJP/Suk6LMveZgxC5nIM8ec/xXPA4GQmEA0VdOybscPE8MA53eL4dUBRFURTl6YSpBZpigaKIApNh12wxzRjQFBdlypQxQrFRo0ZGRDAyA0UFxRmjQASF4rRWrVpGjNoD1iimKE6qVq1qvhOKPoorbodxiBlVgsL9aXB7tJDar/0p3BhSj8KvR48eRljZMapJ8+bNjfhhdAi6D1Dc1q1b1+wjLbAUV/Y+cn8oKBlGjrAcj9EehEY4wI5lGP2B8HxQ5FLIEYo3imjGZqbQZVQHRvqgoOU5poiki0RQKP4phAsUKGAENEO5sSPDAXyE4dzYQalWrZoRcYz2wfNlRyGhMKRIpAC1Q81xHW6P+2BHL7Hhd4pNhoezfdDpnsJrzXXswZmMdsLjYRxoXhveDxxwx/B6vB94X/Ac28dvw/PLEIUUu7ZPNAdY8p7gfcbOGztN9jVnB4vXg6H2eL6YTyHPiB20kLPjwv1gp8k+jxTX3C6vPzsANtxehQoVTDleX14v3hcM6cftML9GjRqmLK8RLfmM1sLzyoGwrueZsEPFbTCKjIa3UxRFUZSIS5i7cDCUF8PW0TXAhsKKwoSWPwoQWkgpKG33BYpJWhgp9LiMIcJoqSW0slJ02JZBRqvgerQksjzro1Ci5ZW+sBS9XJ/uEU+DooxWTApvlqflkGKdgxIpbiiiKZC4zLYeU2wSRrbgMpanwGPECFobbUs394+h8WxxTPFIayWPgeeGFmiKKZbhpCukYcOGRtjZswNSqFOwMxQeLeu0mFJ0cju0cHN/KOSCQnGZNWtWI6J5HJxMhBZ5ikxCkU9xaYtPfqcwpshk/XSFsMPqUTDa56ZixYqPIoK4QnHI+NC29ZbWVwp7dlB4vXg+CcP/8XgocnnO6NZCqy3r5zWnQGYIw+Cw94fWXpbn8XNb7ETxGNhpYj7D1rEjVLRoUXPNuE/sDLCzQyHM68N41zwfPI9cTgHNGM7ssPA4KeRteF/Susy6eO9ypkj+Zdg8WqF5XzJsH/eBnSpaunleeXzcln2ebQHNTgrvN7tjqSiKoihKxEQHEYYALZF0LwjtQXyvAopQWnlp0aQ4puWcVnhO6KE8O7RAc3ITXnd2wCieKXLZyXjVftB8A0ARH9TCriiKoihKxEMFtKIoiqIoiqI8ByqgFUVRFEVRFOU5UAGtKIqiKIqiKM+BCmhFURRFURRFeQ5UQCuKoiiKoijKc6ACWlEURVEURVGeg9dGQDPWru8NX/jd0mmSg+NhgJyfm77wv+tvfZfz5XPdB/fvWJOlhAeB/oG4c+UO7ly+gwC/AGfuf/MwUPb92r1HxxISPEbeD37eL35PcFs8b/dvh995UhRFURQlbHkuAU2x4fbzXIzNOgY3Tt5w5lria+lfSzAm02hcO+jpzP03V/ZcwdBkQ7D872UI8H8siG6cuIFxOcZhRMrhmFNpNqYXn4ZRaUdifs358D7nbcqs77gOgxMNgsfeq/Dx8sE0KTOzzAxcO3LNLCfLGizFmMyjcfOMNeOdK4EPArF71G4cmLLffH5Rtg/cjsV1FxoxHlm4uOUCZpaagUvbrVn/guPc+nMYnnwY9oyxJmrx9/HHjkHbcdT9qBGJYc2R2YcxPMUwbO27Fec3n4ff7WcXuRTEW/tswallJ5+67xTmYzKOlnt3qTPnSXifLf59Ebb22+LM+Te8p4clH4otvaxJfxRFURRFifo8s4B+4PsAS/5YjHk13LGmzWojcr3PW+KWAnpF4+WYkHM8rh9+LGhdubrvKiYXmoyNXTdgdvlZWNt+7SNxQzE+IfcELBMhY4tbCtRZ5WZiapEpuHv1Ljb12GgEled+D+eyWUZwD0s2TITzMmMtXdViJSbkGg/vs9Z+2fjf88fCOgvQ6+OeWFB7vtnu8QXHZd2hRkCNTDMCQ74bjPHZx+HMytN44PcAi39bZJZz2fic43B23VkR4LswJPFgDEow0Pxd+OsC+Hr7GuHe/5t+GJFquNmnjd02wlM6EuwErG27xrkXwIq/l5vt3Tx9E8dEmA77fihGZxhl1mPngOVHZ5TvUgfrn1d9Hm5fvG329+D0g5hScLIpzzQ2y1isbbfWCMtDMw5Zx5J5jNnfod8NwXjpkFwQ4UyBNy7rWAyMMwBDkgzBxDwTcHnnZecePeb8xvMYmXoE9o3fK+fXB3N/nIO+n/fByqYrERgQiHUdrA4MOyjcX9Y1p/IcXD923Vhyj807iilyfe39Y2dqZfOVRoQGB6/5vGruRrSPSDHc/GXnyUOu74bOGzAo/kAMjDfAHM+BqQeca7kg29w+cJu5J7g/o9OPwp7Ru+V83cL0EtPQ53+9zXXg9VnZbCVGph0h53WYKT806RDsGrELty/cxkS574Yllesg6/Mccvmm7htxz+Oe3DMLMSBOf3MthkqZnUN2ODf+mKvSoeM15XqjWIfUzW3tGCpl5fYOuB9gRDiPg9eXifXznB6acdC6/nL8o9KNxPpO643VPShex7wwWa79yDSyPu9HuU9PLT9llrHjOiTJYHO+h8vx8fOCWvNxS86DoiiKoiivhmcS0Hx9vqrFKgyMOwAzSkzHnIqzjaiYWXoG7om4JUZAi3j1EkEVFO8zN42go2B0qzLXCC2Ko809NxuRceOUJaCXixC2YR7F3tzKs41IpOhwFdAzSs0wluD7sozC1haOk/JP/JeAJnc972Ja0alG9FKQnlh03AjGo+7HzHIKcAr2BTXnw//ufXgc8MDqVqtkO9ONJZxW3AAR90v/XIIZxaeLqL9j1oPoHQr/SfkmGkFmQ4FIYbVBRJHN6parzHng+Tg2/5jZ5+MLrem9j4oA5fmh1ZQcm3/UWOtPLTtlylrneyZWy3VY2WQFljdaZvb14tYLODLniKnr5FJLVNGyOqPkNCyqs8h8pzWXovHsmrPme3DYAnrv2D3m+81TN+X8TzTik2KP4m6kiDzvM9a59TjoYUTvzqE7jZjjtZlWbJq5T7h/7CzwXJ9ZdRonFp7A3CpzMLvCLKyS+li3e1U38xbBtuT7iGin8HX7aa5xiVjdajXGSoeAHQjiKdeDy3jvUdiyg3L3yl1joWaHjPlH5TxQzLPs2CxjpNO1CffkuvM88TvvPXbiWC/PK91DxmUbi2UNH993W/puMefB87CnefsxMe8E02EMCQroEamHY0sfywLN7a9ostxs7971e/A67mU6nrw/2BHjeRqdYbR560Jxv2vkLsyVjsOsMjPNuX/g88DU8wj5fZxcctJ0Lvh7GCfieUiiwXD/xd109JY1XIqphac86syeWX1GBPxI7Juw13xXFEVRFCX0+U8B/ZDWx/ZrjbijiLS563EXU3+YgtkVZ+HetXtGGA2KN9AIBQpVPtRniWA6MGm/+U5rpav/8QkRjhSFOwbvMC4XFCrDkw81ddJiSoscBfZ9px/rhi7rzT7YAnq6CPmFtec/8tGlpW/9P+swueCkYF04zP7KPtE6ZwS0bJ+W3iOzj5jlPAa6hMyvMc9YTSl6aOljfbQQbui0way3e8QuI9QpkGil9TzkacQsj/vWhcdWv/siwmmZpqWWyybkmmDODy2eRkDPO2Ysp/xLjsw9Yuo9ueiE+X7U7aixJp5YfMJ0YDZ122QsjNynqYWmmM7KkTmHTVlaoFkXhSq5fem2eUNAoSl6Dlf3XMXYTGOMMOTx2Ou5cmXXZXPO17Zda94o0ErOfV7RdIVlgZZzO0LWt1132MHg9dg+aLs593Rt4fnktTPXUITpfrn2IcH1uY8Ue1Nkn9gBoABnPqFwZwfEtVMSlO2DtpnrMEXOx8hUI0xHh/cYxTUtssYCLWKc9yjPHUXq7PIiwGsvwOkVp831ojvSkvpLnDUCm3tvMueSHQT/e/exSDppQ+S6jMs+1rzhoGuLKxTQrJtvSAjP1fLGy8zbAN5z+yfux6g0IzG5wCTTGeO9wH2lgGfHx1xPOV+0RPP+u3H6sWsUuX/rPpbKfTRSRDp/RzNKTjcdgClyL988e9MIaFqn7Xv+zCoR0HKd+CZBCVsCAgLg4+NjOlGKoihK1Oa1GUSovJ5wIOGa1muM9X7J74tNB4luFOwU0rVHUUKLhQsXInv27Lh2LXg3NkVRFCXqoAJaURQlFFi2bJkR0J6eIQ+kVhRFUaIGUVZAc3Ab3TXo+0uro3m1f8ATblXmGFcJvrZ/0RBtXI8DG+nS8SLwFe/JpSfNK3kOXKPfbdDXvvQJPjB5v/EpXtN6tXHxcN3f4wuOYfnfy437CAdR0o+XvrLGZ+M/8Lnmg3lyTugj/PBBxH7dTNcaumEEB11b9o7fi6X1l5rj57lYQf/rxstxcetFZ6nQgdFI6DZjzrGiBMOqVauQNWtWeHhYbkiKoihK1CVSC2gOxDo86zD2jdtrBqtRYNIf9+DUA8YXl/6mjF5B/9C9UoZREuh3y3UYt5eimgPguIy+yHcuP/a35eCvQzOk7vH7zMAs+qIyQogd8YL+rIzkcHlH8KHh6B5wbt1ZI/C4jh1uj/7Jm0W40v97Qa0FOC3bDy7GMbd1z/Oe+Xx1/1Xjn8zBcDw+sq7jWozOONpE2XiWjgBDu51eedqcqz2j95ioExyoR39nwgFz9I3eM3aPOSf24D4Kcg4MPTjtoPGrPTjtALb23/pocF9I3Dp/CwemHIDHvqvmO4+HAx7twZc8Zp5zniP6IrMsOxWHZh7Cvon7cGnbJRPFg37gDDNHX2Keu6fBdXlcvObBwX2gzzJ9s3nNeV1tNw5GJuEgvhsnvcx3nnuW48BL3j8Mf8hzwOMinoeumegg+2VfL++4jMD7Lx4aUYkarFmzBpkyZcLVq9Y9ryiKokRdIqWAZvQECtgphScb4UOxR1FHYctBi7QO07rLMGm2QLrJqB6M9NFwmRGhFHAMbTciBWMf78FVEaIU1LRcT8o70ZTdN2EfTiw6gaX1l5iwahSQFHscIMdBbg/uPTCDxoJCYUXLNy28HJDoud/T7A8TB5Zd2HbBLN85fMcjARscrHvH4O0mdBwHjjFih22p5ufVrVeb2NZr2qwxodiW1Fssx/Bva+3G7hsxNPEQ7B652xzjlV1XjNBkGDzvszcxrdhUsw0Kaw5uY7SQ/t/2w6aem4xFl9FALjhjMc8sO9OEK2SUlP9i2wBrkJ+HdAAYAo5RXBhpgyHW1ndejyk/TDGimGKZbwX4poAC1Q5leGi6COJ0o4z1neHdQhqcxWvJAX7jssq2RCCHBNdnR+b8+nNGvHPQIiNb8JqTS9IZmpRnohnQyPNtR2gh+0VAc5Dk6eWncVbW5/nmG45z686ZgZVPu47K68H69euRMWNGXLlyxZmjKIqiRFUir4AuM8MIvwtbL5iIEYy4wLBqtPZStE4XsTq/+rxHYozCjKKY4dVs1wvmMWLDufVnjWie8sNknF171ryqZ9gwivPbIpgZxcK2Bt++fNsIaIpzCq8bp24+2oYNrbSMULFZBCgF6vlN503oPop+7tvlXZeNYGT4vZDgMXK9W+e9TeQRRmjgdu0oGKdXnBKBaVnXT686be3TL+7w9XpSQFM0MhwfBTs7CrQ0M2SdibghAppWfIb+M+dyywVjWWYsZtvaS4st40/Tms8wchtE+AYX5SQ4eF7WdViLAXEGmDB2jC9N6zCt7wzHZscMv7D5ghGktNa7QuHMCBeM98zjDs4CzZB9M8ta9wLD17GDwnMX3MyAjGXN8Ikbu27EUambYfXYcbiy94q5J2jBZnxthmdkFA+GTrQ7YAdnHMTIlCOsqCjSAeM5un70OjZ22WBigNOCrrzebN68GenSpcPly/+Os64oiqJELSK1C4dxOxAhREsxRZg9u+EDH38cn3/MTIpii2UKKpY9v+H8I0smxSJDifF1PoWz69TP149fN2KcLg20VrqGqGPM6GMLjpn1Lm2/GKwvNPeF+8R94zYohG0o8ujfzBB4IUGrKi2idGfghBsUa64wXjDrp+g09bvsX3AwJjGt6dwf+k8fnHoQF7dcFIVtLWfs7COzjhiRfdTtiBH+hP7HXGfn8J3m76LfFmFA7P7GOvwscAIehj90dTNhp4WdHhsK3gOTDzwxq6QNOynGfWLqgUezUtpQyLIjsXfsXnMtOJHKnlG7jWvNpW3/9oGmoGfnheeU7iIU5CeXnIDHPg+cXHbSiGDbdYXh6o7IebDdfSjg6cLBfWA95tyP24PDco+4Hovy+rJ9+3akSZMGly6FPOOnoiiKEjWIsoMIldCBIpPCkq4ci/9YjK39tuLa4WsvPIBSUaIqu3btQqpUqXDhwuN4+YqiKErURAW0oihKKLBv3z4joM+cOePMURRFUaIqKqAVRVFCgYMHDyJ16tQ4ccKaEVRRFEWJuqiAVhRFCQUOHz6MtGnTmr+KoihK1EYFtKIoSihw9OhRpE+fHvv373fmKIqiKFEVFdCKoiihwPHjx00c6N27dztzFEVRlKiKCmhFUZRQgL7PmTNnNuHsFEVRlKiNCmhFUZRQ4NSpU8iWLZuZUEVRFEWJ2qiAVhRFCQUYvi5HjhxmSm9FURQlaqMCWlEUJRQ4d+4ccuXKhVWrVjlzFEVRlKiKCmhFUZRQ4Pz588ibNy+WLVvmzFEURVGiKiqgFUVRQoGLFy8if/78WLRokTNHURRFiaqogFYURQkFrly5giJFimDkyJHo1q0b0qRJgyRJkmDatGnOEoqiKEpUQQW0oijKS8LQdZUqVcIHH3yAdu3awdfX1+Q/fPgQXbt2Re7cuXHs2DGTpyiKokR+VEAriqI8Jz4+Phg/frwJW/fLL7/gwIEDuHnzJooVK4YZM2Y4Sz3m2rVrKFq0KOrXrw9/f39nrqIoihJZUQGtKIryDJw9exbNmzdH9uzZjYuGh4eHc4mFp6cnihcvjilTpjhz/s3y5cuRLl06zJkzx5mjKIqiREZUQCuKogRDYGCgCUlXtmxZ49s8f/5845IREtevX0fJkiUxYcIEZ07wsN727dubiB2MHa0oiqJEPlRAK4qiOLlx4waGDBmCPHny4I8//sChQ4ecS/4brlumTBmMGTPGmfN0GDe6UKFCaNWqlbp1KIqiRDJUQCuK8lrDwX30TaZrxqBBg+Dt7e1c8nxwvXLlymH48OHOnGdj3rx5SJUqlcaPVhRFiUSogFYU5bXiwYMHcHd3NwP+KlSogJUrVyIgIMC59MW5deuWqW/w4MHOnGeH+9SkSRMULlwYFy5ccOYqiqIoERUV0IqiRHnoXtGnTx9kyZIFDRs2fCW+x3fu3EHlypXRv39/Z87zc+rUKeM+wtB3oSHqFUVRlFeDCmhFUaI0P//8s4l8ETRqRmhz7949VKlSBb1793bmvDgMhZc6dWps2rTJmaMoiqJEJFRAK4ryzCxdutS4PnCwHBN9fsuXL4+KFSuaiURogf3xxx/x008/GeFatWpVEye5evXqqFGjBmrWrInatWubVLduXZPq1auH33//HX/++adJf/31Fxo0aIBGjRrh77//RuPGjdG0aVMTQq5ly5Zo3bq1maykQ4cO+Oeff9C5c2cTVq5Hjx5GvPbt2xcDBgzAwIEDzYDAUaNGmX348ssvTdmpU6di0qRJ5u/06dMxa9YsE1bOzc3NRNpYuHAhFi9ebHyS6d6xevVqrF27FuvXrzeCdsuWLWbilJ07d2L37t3Yt2+fGWzIMrRwc785KyGt3EwMf8cBg+fPnzeJLhqc9vvSpUsmXb582ZS/evWqEfkMh8e40fxMlxCeb65HH2ta0vmXiS4jt2/fNpZvprt37xoRzxjVTJzMxc/PD/fv3zeJAxXpKkLLNhOjgTCqiJ0URVGUZ0cFtKIoURZXcUhx2bZtWxM+joKWApKi0k4UmRScTBSfTLYY5bpMFKlMtmilgLVF7NGjR5EzZ044HA6kTZsWu3btMkKY4pgimaKZ4pnbprA+ffo0Tp48iePHj5uBjFz/8OHDOHjwIPbv32+EOdOaNWuQPn160ynZtm2bEfCbN2/Gxo0bjahft26dKUOhT8G/YsUKI/6XLFliOgLsECxYsMAMVqTv99y5czF79mxj5eY045MnT8bEiRPNxDBjx441UUQ4HfmIESMwbNgwDB061AyuZIekX79+xhWmV69e6NmzJ7p3744uXbqYjgk7M+zUsHPTpk0bE12kRYsWpuPDDhA7QuxcsHPEQZuMcsLOEztRderUMZ0qdrL4fc+ePeaaKYqiRFRUQCuK8lpBq2/+/PmNsAtNP2OKcApBRvP49ttvESNGDCMyQ8O6e+TIEVMvJ2qh8FcURVHCFxXQiqK8ltAyS0vxokWLnDkvB90j6KJCCyw///bbb8YanTRpUuzdu9dZ6tmgSOashZzApUSJEsaqrIMKFUVRIg4qoBVFeW2huwZdCyhU6WbxMlD00gJNy7YN3TLo/kCXjP+Cvs90jaAbCH2/aXVWFEVRIiYqoBVFee3hQL/cuXObKbZfxuWC/rsU5M/KgQMHzADLbNmyGd9j+lsriqIoER8V0IqiKE4YkYMh7zgY70VgNBEOkgsJCmQO4ONARkYw4SBARVEUJfKhAlpRFMUFRuNghAgO2Lt+/boz99lgGD6u6wrD0zH0Hv2tO3XqZCJZxIwZE++//76JfqEoiqJEPlRAK4qiBANDy9EfmaHanjXyBWc5ZDg2xohmHOyCBQtiypQpxtfaFcZzLlWqlBlkyG0wtJ2iKIoSeVABrSiK8hQYK5luHYy3HBKMET169GgkTJjQTKbyrFE3GF3js88+M0KaE8FopA1FUZTIgQpoRVGU/4ATpTAsHWdbtN06Tp06hWbNmpn4zJwJkROqcKbEWrVqmeXPij3BS9GiRY3lWlEURYn4qIBWFEV5RjgzYL58+UzYO8aPZrxnVzj7HmfTUxRFUaI2KqAVRVFCCU6iUq1aNee3l0ddOhRFUSImKqAVRVFCiX/++ccMHnzZ6bs5yLBYsWLGN7p8+fK4deuWc4miKIoSEVABrSiKEkp07doVVapUCTXL8ciRI/Hee+/hgw8+0JB3iqIoEQgV0IqiKKFEz549UblyZfj7+ztzXp6bN2+aAYa0RnO2xJedcjwoxloegsHc/54/fL188TDg5SzqL8P92/dx5/Id+N7w5c46c/+b+3fvm3UeBj59nQC/AKvcg/A7RkVRIh8qoBVFUUKJvn37omLFiv+K+xwaLF68GN988w1Sp05tIoCEBhc2X8DI1COwofP6YN1Ozqw8ja19t+LetXvOnLCD4n1etXmYWngKji84hmtHrzmXPBvH5h/DjiHb4Xfr6ddibbs1GJFqOLzPeztznuTk0pOYU2kOLu8M3Y6LoiiRGxXQiqIoocTAgQPNFN2csjsycHHrRYzJOBqbum/8l4DePXo3BsYdgDGZRsPrpBe8z3pjQs7xGJlmBMZmHoPhyYdhRMrh2NJ7MwIfBOKe5z2sbL4SY7OOsVKWMZiUbyKOzj0SrBX4ge8Ds+7ojKOMiB+ZagTGZRuL/ZP34/qx65j6wxQMiNMfQxINxpyKs+F97t8C1/uMN2aVnWn2ZUyGUZhefBpunLyBbf23ov83/cz2b1+6jfObzmNqkalm30elH4mhSYdgUv5JuHboGjZ02YCB8eQ45TyMSjcSQ5IMNnVeP3LdrDdGjmNQvIEYlnQophWdimuHn0/IK4oSNVEBrSiKEkoMHToUZcuWxd27d505ERtbQG/uucmZ8yRr2q42opai9Nb5WxifcxxWt1rtXAps6LwBo0W4ehz0wPK/lxuRubjeYqxqvgorm63E0vpLsf6f9bhx6gY2dFoP91/cMb/GPByddxT7JuwzQvbEohPO2oDtA7YbMUzLONfhvtE6brNnzG64V3U39WwftB3379w3IndZo2UikKdgWYOlZj2y5M/FmFxgsnH/OL3iFMblGIfpJaaZ7Y9OPwrzqs/DXY+7WNdpnRHW7CAQimp2DLb222q+7x65G6MzjTL7pCiKYqMCWlEUJZQYNWoUSpcuHWZRMw4fPozPP/8c3377LVavfixsnxUK6FEiJkekHGHE5uSCkzExzwSsarnK+BBTQI/JPBo3TlgCemy2MUYY21Acj0gzHDfO3DAWYvdf3DAi1QhMyjsRE3OPx8zSM3Dnyh1n6Sehi8Z6EdW0+k6QsuOyjjXborB+GBBorNBctr5jyDNA3r54G25V5hphPz7neCPmD886bCzei39fhImyH9z+6ZWnMSrtSIzLPhYzSk03FmZ2BG6evol1HdZheMphppNAPPd7YliyodjSZ4v5fnHLRWNxp5V8yg+TcWLxY8GvKMrriwpoRVGUUGLs2LEoWbKkGfgXVtAfOlOmTGaQIf2vNeTdv7mw+TxmlJwOt5/dsPTPJZhWeKqxrJ9de9ZZQlEU5flQAa0oihJKMNQc4zd7eXk5c8KO0aNHm5B3sWLFwpQpU5y5iqIoyqtABbSiKEooMXXqVBNy7vr1686csIUTsJQqVerRBCyvIhqIoiiKogJaURQl1Jg5cyYKFy4MT09PZ46iKIoSFVEBrSiKEkrMnTsXhQoVwtWrV505iqIoSlREBbSiKEooMX/+fBQoUACXLl1y5kQMli5daiZgadasWajOkqgoivK6ogJaURQllOBsgfny5cOFCxErZnBgYCA6duyIGDFimNkMly1b5lyiKIqivAgqoBVFUUKJ5cuXI0+ePDh37pwzJ2JBy3j69OnNIMMKFSpoyDtFUZQXRAW0oihKKLFmzRrkzJkTZ86cceZETMaMGYN33nnHJPptK4qiKM+HCmhFUZRQYsOGDciePbuZ3CSi4+vri7Nnz5q/iqIoyvOhAlpRFCWU2LJlC7JmzYoTJ3S6Z0VRlKiMCmhFUZRQYseOHcicOTOOHTvmzIlcrF27Fp07d8bJkyedOYqiKEpwqIBWFEUJJXbv3o2MGTPiyJEjzpzIxaZNm5AoUSIzyLBRo0a4f/++c4miKIriigpoRVGUUOLAgQMmysXBgwedOZGPgIAAtGvXzojor7/+2gyMVBRFUZ5EBbSiKEooQctz2rRpsX//fmdO5IUDIWlNp5CuVKkSbty44VyiKIqiqIBWFEUJJTh4kDP+7d2715kT+aEFevz48fDy8nLmKIqiKCqgFUVRQgnGf06RIoXxhba5d+0eNnTdgGnFpmFK4SlY3mgZruy54lwKHJ9/HFMKTcakfBMxKe9ETMg1Hpt6bESAX4CzxNNZ23aNWf/2hdvOHEVRFOVVowJaURQllOAU3hTQO3fudOY8yZ0rdzBVRPT04tPhc8PH5O0bvw9DkwzGntG7cWHjedy68PTZAX1v+Jp1lokQX9F0BaYUnIzJBURAX7IE9MVtF7Gu4zos+XMx1nVYiwubzuPhw4cIfBCIs2vPYHXLVVhafylWtViFedXccWnbJbPe83D+/HkN1acoymuNCmhFUZRQ4vLly0ZAb9u2zZnzmLNrzmDJH4sxNssYrBbx6uftZ/JvnLyBw7MO4fLOyzi96jQmF5xkrNFex//tMnFq6UkMijcQm3tuRsD9AAQGBBoxPLnAJHjsv4rZFWZhePJhxiq9a/gurG61GoPiD8TCuguxbeA2DE44CHvH78XN0zexuN4iU/bS9mcT0Hev3sHxecewvMly/JL/F+MbzWONSu4qiqIoz4oKaEVRlFDC09MTyZMnN+HgbG6cuoEdQ3bgqPtRHHE7guklpmN0ulFG8JKjbkeNmD3mfgx7x+7FmEyjMafSHGOtDgrFLkXv9BLTcGT2YRxfcBwzpD4KaK8TN7C84TJZPhRb+23BuXXncHTuEZxbf86s63nQE1N/mILJ+SeZ7W3qvhHXDl8DHprFT3DX467ZXyOyUwzDgG/7o9/XfTEs2dBH9e3ZswcJEiR4FPLOz8/qECiKorwOqIBWFEUJJa5fv45UqVJh3bp1zhwLX29fI6Rpbfb1+vfU2XTLuCEC+ObpG7h/+79jL9/zvCeC2Qs3z940yfuct3HRILRM3zp/C17HrhtLs+9N2Z6IZL/bfiK6j+DQ9EM4tfwkNvXYhIFxB2Bjt41mvYdS5uD0gxiRajj6fdnXLKP1momfR6YdYdxBXHnw4IGZeCV69Oj46quvsGLFCucSRVGUqI0KaEVRlFCCkSoYxm7VqlXOnIhDoH8gbp65iROLjuPQjIPGpYTCPSh3r96Fe1U3jEo30ojnAbH7Y3T6Ubi867KzxL85ffo0qlSpgnr16uHOnX9bzhVFUaIaKqAVRVFCCcZKzpAhA5YtW+bMiTx47PfAnEqzsaHTevjftazgPl4+2DF4BzwOeJjvEYFFixYhX758uHjxojNHURQl7FEBrSiKEkrcvHkTmTNnxuLFi505ERtG5zi59KSJCrJvwj5nbujh7++PwEDLtSS0WLhwIfLnzx8uAppTmx8+fBi3b2vIQEV53VEBrSiKEkp4e3sje/bsmD9/vjMnYsJBgiubroDbT264vCNk14yXYdeuXWYqcPpHd+vWzZn78oSngGac7xw5cmDt2rXOHEVRXldUQCuKooQSt27dQs6cOTF37lxnzjMQTBSMVwH9nXeN3IVZpWZi57CdeOD7bBO1vAwcZFitWjUTqSNlypQ4cOCAc8mLs2DBAuTKlSvcBDSvrwpoRVFUQCuKooQSfLWfN29ezJo9y5kj+jjgIXw87+Hi1ovYM2aPCQ3HWM+MdsFBenSheBUw6saJxSewuO4izKvqjmPzjsHvVviEmqM12g5599dff72UWwfdTijMwwMV0Iqi2KiAVhRFCSUYgaJgwYIY1WckNnXaiBHJh6P/t/1MWDhGs7DDwrmmJb8vxubum7BrxC4TRo5RMs5vOI+re6+asHeMnOF91hu3zt2y0vlbJjzd9aPXjSg/5n4UO4fsMDMLLqi9wIhlzkB4esUpK4RdBIGit2PHjvjggw/w66+/Gn/iyAat3pUqVQp2opywgGESNcqJokQMVEAriqKEEnfv3sUPP/yASZMmOXMsaPm9sOkC1ndch4l5Jhjh3FdE9YTc43Hv2j1nKcu6Sot1gH8AHvg8MNN901+Zk6pwqu7bFyXJX65DC3OAXwAeBoaRD0gEgQM02Um5dOn5pyCPzPDeKFWqFHr37u3MURQlPFEBrSiKEkrcu3cPRYsWxbhx45w5IeN/199MnEKxrDw74TmIkFZ0btfHx8eZE3ZQQJcpUwZ9+vRx5iiKEp6ogFYURQklKKxKlCiBUaNGOXOU/2LQoEHGN5qi+FmsyuEdhYNRVtasWePMCTtUQCtKxEIFtKIoSijh6+uL0qVLY9iwYc4c5Vlg2L/PPvsMb775phGIFIshwbKMwnHhwgVnTtgR3oMIGdFE7y1FiRiogFYURQkl/Pz8UK5cOWNVVZ4Pdj5q1aplrNHfffedmbAkoqFROBRFsVEBrSiKEkpQQFesWBH9+/d35ijPCyNc2CHvRo4c6cyNGNDqzQ7S1q1bnTlhC6eK50BVRVHCH527gP0AAG+1SURBVBXQiqIooQRDs/34448aKeEVsmTJkmf2l45K0K2F/vW9evVy5iiKEp6ogFYURQkl/P39UbVqVXTv3t2Zo4QmjIJRvXp1vPX2O5g0aaIzN+wICAjA5cuXzZuGsEYHESpKxEIFtKIoSihhT13duXNnZ074wCF4z5siMpy5sEuXLvjis0+RrGhlVJm6BfFTZcCuHdudJcKG06dPI2vWrBqFQ1EUFdCKoigvwoNA4LY/4OEDnLsDHLsJbLsaiGKN+qBC5ymYdBwYcgDovhtouw1ovAn4Yx1QazXw0wqg7BKgyAKg0Hz5uxAosRgoLXnllwKVlltlqq4Eakj52qLX6sm6DTYATaSelluAdqIdO+0Eukn9vfcAA/bJ9g4Cow4B444CE56SJrqkcUesdYbJugP3A/2lnp5SZ+ddQHvZRqut1r7/uR6osxaoKftTbZXsn+wb97PCMqCM7HdJ2f+ichw8Hv7lcXD/uU6DjbLPUk9n2V9uY6xsc/ZJYOVFYIeHnDtv4OJd4KznLdSqWQO5cmRDqXIVULZKVZSu+CPKVv4J6TJnRbxsBVFvzQW0OiXnb+gCxEmWCkVLlTVlSleqIuV/QZFixZEhQ4ZXEq0iPAcRUkD/9NNPGDx4sDNHUZTwRAW0oihRHk7Wdz8AuOEnIug2sOcasO4S4HYaGH3YErlNN1vitooI13Ii/kosssQgU0URiXVFM1FMUlxynVkiAJefB7ZeBQ7fAC7fA677BKLGb3+iZbuOCIjoZt1wxL4ed6QDwmtyXq7J/uvAhivAUrkus3ZfRYv2nZEqWx5kr98Zf2z0REs53y2kU9JMzj1TcxHhLU9I3jHgl9m7Eb9oVXyWsQg6jZmLU15+8JVtsJMTmmgUDkVRbFRAK4qTqfIgplWQD3Ml4nFXxNZVEam09FJozTllWXjbbgd+Ez1TXkRuAQreBZZF9OeVkr8O+GeHCF4RW0tF7O4T4XzqFuDpY4k3fxFYoTkTNq2E9erVQ8uWLZ05ysty8fw5pEiVGkV7TjEimqmVdHwonpvs90fSkr+gdo3q4HyOd+S/S3eB43wb4AHMlXK0eDffYnWOKi63rP0F5lmWc1rVu+0CJspvf/VF4KisxzcKFPfBceH8eRQrVgybNm1y5oQtnOmSA1UVRQl/VEArURJa/9bIA5GvkNPOAFJOs16fn/R2FnCBAqrhBiDaECDGMKD/XucCJdQRfQlfESfXfIETci0ocvgqv8duS8z8KAKHlt98InCKyd86a4COFMCHgYVnge1S/owIYC9Zn/VERP788080bdrU+U15GehTXqVKFWSq2wa1Fh9Huip/IHbCJIgV8x0kTJMZ+dsMQe0lp5Awxw8YN2aMc63nh+3FTT/grHSe+UZhtnTOBojwpusKXWny228i5P5sIGK87z5gkdyPB65bbx7uPbDu7VcJO2fFixdHz549nTmKooQnKqCVCM11EUqHveRBJYmWIfuV7GkRUcVFYH0yCkg0GUgwybIeezuNM51EdDkGyANwo/V9lycQaySQx816ZWxz/g6QW/J+lockt8F6Uovgpj+m8t/4iYilNZev3+eLoKC1jz66PzpFxw8LLF/YGquANluBEYeA5Res8hfk3NOHOLRfs4c3DRo0QKNGjZzflJehWbNmeCdmTPz008/YvMn6MS9duhQFChTAVQ8P3Ll9B1MmT0amzFnwySefYNUqudFeKQ9x3+cOAgIe4L7ct+wI0n1nldzTww9agpsuQOz8sRNYWQQ3rd8jZNlKKcO3JxTqL/LWQwcRKkrEQgW0EqYEBBFLfI3eWh4wVeWhQ4sk2XAZ+G4q8OZQyxrJAVKdRRA332yJLvLXerl5B1uDqSjCgkKL0owTQJwJUm4QEEPqonW5pjxf+QqfbL4CfCAC/H0R1lnnyDaniCAfbZWPPxGYd9oq9zpBQUxRwAc9fYRHiuBtxuuzEiglHRRa4cqKIKa1mNdl5knLKsyOCF0sFBFRjRujfv36zm9KaLNw4UITB/rixYvOnMcwWsfw4cPRr18/3LnjbCxCkZeJwkHhzLaHriJjj1o+9+xcFnS6HPFtS799ll8935TdvG+1Y495iLIqoBUlwqACWgl1bknD324bUFjEFkWYzd7rwJfjLP/DK04L705P4IuxlhWYr+U5qOvdEcAPsi6/29BXlQ8UWi4PelkWnM0itBmVIOMs4EMRwm+LQM4kn/mAohCkO8BbkkfLD7kj69PS/KbkURiyDB9qrqKewjHRJCDNDMviHRXgcV6VY9l2FZh63PIJrr7aOse0lDGSQn05j333Au5y/imI2VEJi9fSURG6b9APWnk1zJ8/H7lz5zazAgaFAnro0KGIGTMmPvzwQ0ybNs25JHQIi0GEdE3iQFcaEsYctoQ2f6NFFjzEZ1nKIc9ffTFQ2q8lIrRPSzn+ThVFCXtUQCuvBLpSMHJB9MFA111WHkNmxRRx/NZQy9K77Bww84QlfOuvp33F8od9d7g1GOy6i6vFpGNAXRF934oAp5vF3mvOBS5wgFnyqZYg52vVRWeAr6X8e7LNrLOB72UZt19tpeUaEpmhKL4ix8sOBQfTcSAUQ51VWGqFRmMUCZ5TWxSz88Lzo5EhXj0cQFinTh3nNyW08fX1NeKZYjkkrl27hiJFipjpwPPlyxdqsxZGpCgcNFSww79U2tE+8jtnlBh2iPnWjqEPOa5gmYhs+nXfVZGtKKGOCmjlubjmA8wXYTrsgCV+bZeK4KBWo18grcC0dvJ15WdjLNcJrv+OCOVYImj5d/Qhax0KPMahdQwB4otQniLCmdZTWorXXrSEMH2bu+y0rNi55sr3QSLUZRuxJwCNNsoDw+miERmhPzCjCNCKzri8tLCXlAdiQTl/jLPLaBN8MHKQE/266X8cmlEklJendevWqFmzpvObEp7QWk3f6Lfeesu4PtCP+GWggM6VKxfWrVvnzInYMJrIERHZC85ahgwaDxiFhO0J43NzzAIHW2s7oijPjwroSI6fCC5aGF7mNR4tk/NEFFO02c8XWjco3Gjt3X/NGm2eZDKQboZVjtscf8QSxCmnWxbfkKDLBa2/jv6Wr7Gn0/p7SOpkdIyPR4uovmrl2dBlY4vkdZdG/095VvE1Jt0udsu+REYr6m05nydF2NOdhA+t39dbr2U54QStxn+JUGbHYbE86PjAY4dBiZy0b98ev/zyi/ObEtrQ+vvjjz/Cw8PDmfN0fHx8MHPmTCxbtsxMxR1ZofgvUaJEqEfh4KBqvqGacdJyveMgSIrsysuAFluseOe0dHO8iqIoj1EBHclptsmyyNKi+zRWnLcGydG9ofwSIAstuYMtqzAb0DnSSL4/whLIHBC2+BzwwUiglTSghK4ALE9f4+wigjnoj5EuaIWmO8V/Na4+IvA5SIaD/lz1L8Uww0BF1kgM7HDwfDHGcD85R5wtjgPt8rpbr1L/EKE8SAQzX6XSr1GtPFGfTp06mRnjlFfD0wYRRmXCMwoH2ziGkWRIScbPzi3tGyPsNNlsvSU8euPJdl1RXgdUQEcC/AOsUG6Tj1uv74eIIDsk38kxabg46I0uDxTFfOXPCQO+EqH81TjA7Yw1opvuDQmlnLeLZXOWiF+6V9ACSp9aDl6hYI45XISyiGnWe8oZGYMCmbOw0YeYluhyIsLzugGfj7FeC7oO+IsK3JPjpcV4xQXLMkwhzM5GsYVWiDa6igyWTssqeYbzHKl1RrHp3r07KlWq9FQfXeXFCQ0BzclI9uzZE+xAxKfxMlE4XpaIGsaObws5lT2NBHw+VV9lhRjlOIyG0k5y/ApDhGqUHiWqoQL6BeGjka4JdDN4EZcCNjo7PKwBYKzjaZZJNk6cJY8DxmjtZSg2+v3WlTacPm587cYQbYNFWNtwEB+F7rfjrf1k5AWK7B+XWbN0UVRTaL8x1PIntl03CC3CpaQBpNU5KsKwd4z+MUU6JK3l3FWSc5J/nhUdhINvOFUzrS10U1EJpDwvfMVevnz5SO0uEJFZsGAB8ubN+1IC+ty5c0ibNq0ZZFi5cmXcuvVsAyfCcxAhBXSpUqXQu3dvZ07kgQOe2aa23269mcvjbhluOsmzZ6n0YTjORVEiGyqgg0BL7OW7gNd/+KBy0EXq6VaUB/oHEwozxvCkHyuFLf3KOIvVT8tFzE4B4k20rLsUrVx3sohiRp1IJssY3o1hi4LjyA1rNj2uz0F5FNLFF1rRKxgmjrFFOZkIXTTcRJBz+wzX9rZsi77D9oxtdKOgRXXAPmDUIStcGYV8VIF+xpyKd4kcP2cKozsFJ1cpKg02rwPjGY8/aoln+n1HpWNXIg59+/Y1AtrfX01urwL6NFPIhoaFf/To0Xj77bdN2LsZM6SR/Q8iUhSOqALH29BCPeaIFV++1GLrTR+n4edzasuVJye/UpSIwmshoGlcpQjldMC0xA45YFllbbh8kgirT0cD2eZYveQf5snJGQzUXh1yCCBGjmCZppuAtSJkvxxrDbyzxTfdJRhSjG4OG53i+Li3NUkH4xXTskzmn7ZiE9MVggI+KLQ6JxaBzMF2FaXXntPN8lXOLHXQjYIWZcb3pQ/uetkPJkZyiCrQws8OCy31dGOhKwljPBeWRpaJo8k5AQHDOdFqHNVmtlMiFwMGDEDZsmXh56dP/ciAp6cnSpYsaazRjLBB63RI2FE4VECHHRTPnOmx1x5rZke+LeRkTm23AXPl2cm3qWoMUcKD10JA0yL7h7R3FGAUWBTFHHhH4UtotaQFmNEk7KmgCQVp9CFADRG2wUW54GspE0ZtoGXt5QQgFMd0DbDdOuiiQXFcXeqgLzPhlMZcZ6CIPsIpYRnm7X8iwHc9ZWA5qww6k19kh+eb/t0MjceZ7X5dY/nPMToFreh0sZh2wrK6M4SeNpRKRGfw4MHGV5XxipXQZ8OGDWaQ5rNG4XhWli9fjuLFi2PsWGmIIyB04aDQ79WrlzNH4XOZY1X4nOXbVgrrQguAWvIcGXoQ2CrPfI1opLwqXisXDs5k13AD8IEIXVqF58mPjkL3hjznOBMe/Yj5+t+Gr/m/n2a5aey55swMAl8xUSA3kx8v2XQFyDDTim3cVoQyZ7PjoIo8Ur89hTRdDXY7Y/hGVWhJv3hXzoc0YBOOAi3k/DAsEoUxE8O4MToFXUrYqbHdTBQlsjNs2DDjq3r3bhR6DRSBCO8oHPRtDw//9og6iDCiQoMTn+F8xnTeaU2Xzsghv8jzuPde61ntIcudti5FeW5eOx9ovt6nuGOPlTPU0ReZQo+Clj7GjFax5JxVhhN+UDwzLFlIM9fR75mRGOgi8iKDCSMj1+RcmLihJyyXGPoXc+ZAWo7ZWeCgRA4YYexQdk4eaAulvEaMHDnSWArv3HH6aCmhSlgLaEbssDl79ixSpkxp3D1++60uHoShkFYBHbrQ1ZLzCtCQU33148mqWm+1nl8MO6ooT+O1EdAMM0aXiUGSxh4BCsuPJcZQy53DdttgJIwFZyw3gtLyQ2q+2Rpo9zpAjcswQ2w02DMfedgKQVRumdWwcOQ0v9PiTh9rzkAYnL+2orzu0AWAE148a2SH4GBnnO5KfDPDtothIhkdh79Pupzt97Jmotwm7dP6y1YIMbfTwFTp1LJ94zgPukTR8sYoPRw3wFfcDTdZA7U47TOj8NSQDi8tcj+v/Heq6kzB5f8iqZqsV1Pq4BTyHPBVfwPwt9TfQrZF/9Quuyw3uBEHrWn8OSHHIhEmnPmO7nQczLtPOuI8Hh4Xj4/+rmyH2LbQ2BFcdKJlixegQP58uHLp1QvoQYMGGbEcJ04cbNy4EXt370H8pMlRevB8JC5QBgP6hp2YpYAuXbq0CugwgIYxjj3i5F28x/PNsyzYvLfnyz1MtxEOyldeb14bAc2GmJbTE96WK0VIFuWoCP3E+IDiQEdG8eBDjj3tvByMIY1CPXmg2lO68tzQxUTaakVRngJFLsUtXbE4IJhvZdaLMGw4fj1S1O2HdhvvofkW6ZCLWK0oHVHO7sYJKPJLh5SRYfjb42BYhk78XQRoS3k4M44ufTcZocddOvP8TbITzygFfKPD3zEHCLMt4yBlik2KbIpt7g/buYj402V7wv2jKGaEIrZJNFywHaZwphsXj4/HuU3OIaMZzToFjJGOPMNpdthuxbivKWK94vw7yD/iMArPC0A+OZectIjtGTsC7By0k7K0KnLsBF/f0/2O9fOccbv/dX7mzpljpmKvX/8v/N2kKSpUqGCmAqeQfv/jT1C48xi0ks5AnRVnECdtNpQuVRINGzaU8vXRoGEjNGj0N+rUqYMOHTrgxo0bzlqVqAKF82l5TnL2XnZKGTWEApt+1+y8PsvEYkrU4LVz4Ygq8CHAhydniOIDh37GTUQY29OwMjE6BWMa84fOqCOvU6dBUUKCIpOik69wKaz422A4SEay4Uh/vmmhGOOMa3RLKrjAEmi0uHIMBcXcoAPWYGG6e3GgEq2oDH9JUTh24hQUL1YUPt5SsRJusFPBEGkU6BTndMnjq3mGsuR1ZntJlzOGTLNf33N6/boU6vM8kabeAMRKlR/pa7fGHxs80FrWbXUaaC4iqZkIe6aWItLbyD3Q9NBDlOg/G9/nLYbqNWtj186dzr1QXifYQWQnl89cuoIwKldhaT/oIjJMOsbsDPM5/F+dOCVyoAI6gsGHOx/CfCCzse+/37Kq0IWCvticDY/WKsZy5vTR9L1m+eBedSpKVIaWTI6w51sTvl2h1ba7dBjry++FFl9OjMOHFy297Fj+Ib8bTtwwSoQPf1t0f6Cw4kBf3weh9xuaNm0aihQpgmvXQhh5rLwU27ZtQ7169XD9+nVnzqtDbjF4S2+rbt26iJenFBrv9UULuc8onFtIB6qF/C3RczLe/jIxCo44jFZyfw2QNpvx/bc7482H1qt+2wc6Mk6koljtC9sazvfAsKt0g+LYIbqGcCwRn+fs7OmzPPKgAjqM4NTQfM1La/FEaYBbbLF+QHz9Q2sxP7PHOv7I48lR9DVQxIGvfukvT79R9X0LXfhqn5ZCvk2hGwStuvTh5evRanK+aQlm5BZ7kCoj3rADOfsUsFl+T/yt0EeY9UQEZs6cicKFC4d6mDXFIqwHES5ZtBDxM+ZCrcXHUWbYQnxfoBTSZsyEZJlyIFv9zqi37grS12yGer/WktKU3NYbDoY5pfsIQ3TSRY7T/zOOMWPXlxbRxDafkzvRTYV+7HQvZIcwxEHXOogwSsNrz9mJRxwCfltr6QLeJ403WUEPeH/wvlIiDiqgXxC2cbRaMYIHrV9sBNtsg4ldzNeBvPk5VSkH1rDx5OCZQzcsoaD+xWELT3fQU77ygjW7Y6yR1iyO7wyzIrCslvygcKKa9DPlxzIY+GS0ta7ydDgIjL66HJBK9yJaWDgYh+KBoaT4YODgM1qEuXyN/IZsN6PIHut87ty5KFSoEK5ckYNXQp2wFNA7d+5E7Nhx8OU336Jjhw5Yt3YtcufOjXXr1pnlvj6+mDVjBvIVKIi333kHXbt2NfnPi+1XS+MJDSx0E+IATxpYCs6z3EsabnyIpHnKoGGHPvCQ5wjnD1BeD/i2jW/LGPmKBgQaEzihDAcDc6Aj50nQQf1hjwpoF+yHPkeGz5UeX4891uhyWg3oQsHGjAMFOFMhBwuslsaO4uq/pv1WXg3ssTMSAS08y85ZDyC+/qIfWvddwMejLFHMV/mZRACz8SHs+NSR60hB/PdGa0Q1/74lIppvAFxxPw3EkTqmHZfrLc9rxvfmbJDc9uvUDzJvUG5b/r5T5AHfUQQxfwt0laAPKQUxfe754De/DelkHJMOIwXx6/ZKcv78+ShYsCAuXw5hbn7lpViwYAHy5s0bLnGgg5vKm1OLc2IXTgfeokWLJ8LehS4PUbpkCbTt0hPHpM2iG1KfvZaLH90AiskzioNSG22yRBV9vvnWU4VV1Ibt61m5znxzx6g79OM3E5GttCLhcCAyx2eoa0joE+UFNHv2fOizV09rF0PU0TrMUbP0j6SVmK/W+ErYTUQzR9AydrESPgQ1qqw4b4lfurcQ9sQZXvDNIUDyadYgSYbvYng9+h0SvupKMAn4ZIzlFxvSq32KYk6ek2GWNdiDccEplikQuZ322yyR/anUw2nUY8lyWqyjybb5poGDRSI7jLjCTggH0NFKzEaXUSKY2Gn8a4Plh79IGufDIojpyqI8nfCe6COqw6m3KWD9/cPexy04AU04sUrr1q1NpI4vv/zShLwLb/jsO+RluToxugsHwfLtTx53ayxNB/m9s+20DQ9K1IT3AUNGMpwk9Q8t10x/SMeLBiMaASOK+1tkI8oLaFoj6TahDUTEYeNlIOtsacSXWINsbPhq6g0RrC23PHZz4Uh5TntOqyZhZ8cxyJqsxYbXmK40W69YkRHYCeIIfIawYvxbWqA/ExEcfahlLWUMazYanHY92VTr1RhhWDBOrPPBKMsXLTgTM3v5X48XYSmNjz01e0SC540DVXgOGHeXFgmGUSvvtBTTOsFBdoxCQOs637awPM+hEjosWbIE+fLlw/nz0vtTohSnT59GlixZsGaNKJFgOH78ODJkyGCE9I8//vhSscDDAuM6ctuKI87Z+fjGlW9a2XlmeMWuuyz3w5Pe2nmOithRQ/hcsw0oNDDyTQbfMi6VfEYqUrfT4FEXDiVcoM9WfFqJRaxuFOHLwRGMMvLuMMsfOfscywWA/n8UtBx8SfgjdwywIirY8CEw84RlmY453LKwcFBZUMYcssQ4B2gQRjqpJMIytgjiz8cC6WdYk05QYEdEGLaQM2Yyvi0bt5+ksaO/Pa0JZZdaVnr6EzNUkj05kBL2LF++HHny5MG5c/L0UUKdPXv2oGXLlrh509nzjYAMHz7cxI7+/PPPsW/fPmfuy8MJenr27On8FnZQZNFVrpO0O3Rp5Btctj30wWXUEUaWoKFKiVrQMs2xKWOOWG8jec0Zd92eDp1jVzj50euKCmjlhWCHlBMTMHKCDS0VDBkWdyLw1Tgg91zLHSIkH7w70uByJDr9isssBv4nIra6fOcPksLWMUTSYCDzbMs3nXDgDK3S0SU/+VQrWgMHqnEgJ33TPxpp+T5vkO+LpMGnhflbEcjfy18OYmNDH5HggDkeG92M6G7CGdwYaaI4rUCSOJCIg1PpYkFXC1rsaV1XIi6rVq0yApqv+5XQ53V1kYnIU3lzrAPdBEYfBv4QoWX7ZLPNpZ82B17TH1vfBEct+KxmpBledwpsjoXhm04OEOcspGvlJ2o/u6MiKqCjMAyDx8EkrbdY1stngT1OWnTtEd78222XJUT77HnsKzVchCutuX0lj5YH/mjoJsFwO7Qu01rx0wop09/yL2adIcFpfmk5pm8xBbENrcr0S64q9QQXvoc+ufTh4kxl4+QHTLcLe7/DG54nil1OWTzBKYxpMS6ywPJD5LmhFZkDG/fI+aIvshI1oH9srly5cOqU/BiUUCc8BTQ7RdmyZQvRheNVEpEF9H/B9pvPBbb1dMPjTJyFpB3kWBIO1l98znrzF9kj8ChPQrcfGn4Ye5/uQT+ITuAzkBPLUGDTdYRGuMhqFFIBHYXxk5u3rrTzMUWE9peblZFF+AqOfm30bbJ92ihu2ahRrPLmpitEPnfgjaHWoANGraAFgb6/DP22/hKQc641+I6N3l1ZzkEptBbTesrpeNkzpeWZy59F1FIM07WCr4tcoY9WRBtFzggcB+Rh4C6dBHYuGBua1hZ2Ivhqi1MJTxdhzGOilT7EuK5KlGTDhg1moNmJE3ITKKEOBTR9zCNKFI5n5cKFC/jhhx9M5+pF3DoooMPLheNVQ2MPXerYbvJZREtm4fmWJbO/nCq6+Xm4jJdRoga87hyDxMGsfNPKCa9oYOKbbEbG4qyhdN/09HGuEMFQAR0F4AC6WdLwNHVOTdtRBBx7+4SuAV+MsfyNKZp5w1L80U+YgpfRK+bJzfvWcMsq6ir2aDUNOmCvhwjGGCKsOSBvmIu1mK/m+Bony2zLZYLbyygCm+4WHLAXGWDkDQp+Ntbj5IfLSQ7skEAUxwwXRQs5w9mZjkEEE/ZKxGDLli3IkSMHjh075sxRQhOGB2SoQD+/sHe+fBkBTXbt2oU4ceKYQYbNmjWDr+/zhXwKDAw0Qvp1gy4idNXjDH5VV1rjZSiyOCEZB0trhKCoCXUFrz2fyZwKvd46a5AjDVYc5MrB8AvOWDMymzk2nOuFFSqgXxGnvC23Al7YF4EDwSjWBkqDsUVunqf5jnFb3A6F8UxpTGgdpnsFe+6EVuQ3hjyOg0zoC/z+KMviTGtxTRHeFNQsyygZ9LlNPBmIO8GKJ+oKraq8aZ/VLSQiwGPkLHd0MWE4Q1qK2Qjzh8jwToxWwY7EcTmXLKuvEpXn4ezZs0Y479ixA2PGjEHKlCkxZcoUbNq0yYgtLldeHp7Pfv36hYt4JozCkTlzZqxeLU/vF4Th9zp16mRE9FdfffVSdSmWewjdAOgGQism4/Tnd7eMH5wPYPkFy+ChRE34Bp1GRM5KO2j/47joHOjKWWzZydrGqFqvABXQzwAtjRflB7j7miWyGB+4rAgvxiAOSdgyJnF0Ea0cFGeLMQrh3tJj4l8aEehOkXEmkGo6kETEKhMHzkUbak1IwfAxtPLS2lt6cfCClZtniDe6XzCmNR36GcKMMZK/k/oY45N5H4lYZixjxr5mqDYOtGNDwxvPhg0RozzQL4mWawrJiA5/PGw8ja/xUaDJZmtyD854R3HMH9Nw6bnaVuOn+WIryovi5eWFFClSGFEUNFFwcbnycpw4eRIpE36PxB/GQY3q1XHnTviootCyAh89evRRyLuaNWuaCVn+iwoVKpgOhPLsMCIRx8fwOcAJtBjWlDM7csIZGoo4Q7COQVFeBBXQLtCR/R8Rrhzo4Aon5qC4/XaCNbEHf2z/5ddKsVtUxCon3lh81hos8fU46Q27hIalkKY7BAfZ2U70Q0Uw03rMcGqEPsC/yLosRz+h4GD0i2/GW77OnJaalmO6YxST7dOPiBPD8DVIZBOP3Gd2Wmg5Z4eCsSkZQofTmHJ0d0/pjCyV80kLPBtJHeGthCd02UiZMhWiRXPgiy8c5m+yZN/jpAg/5eXwuuGFPLnzYHKFnnjQ9RCyJ8qAcROkQQ1jKJ7p2x6a4p2dq9u3bzu/hUxkHkQYUeHzlbP00cDCEKkMB0r3Rj4/6S6y6arONKyEjApogX7B9BumlZY+vymmWW4KrnAmJ8Yf/kAEMaeHNmWHWOHWQnJwp28WBTRdI4zAHQ5km20JZ0LLdBURhbRUUwgSTpdMizTDwNGdgHDQHkPDsfcc2f1uqXHZAaFlfN1ly6+JVuJy0nBx8AAt7X9vsqzqXE4LuU5Fq0QW2rfvilIlHLh1w4Hq1Rxo1Kilc4nyX9y8eRO1atXCG2+8gcTvf4vm2Wqh7w/N0aNgY3Qv8DfW1pVGsMcx6Tkfx9U2mzC8VAd0y98QvQs1RY8CjVAyQW686YiGJN99h0WLpJf9Chg6dCiiyzaKFi6CBw9erUWCwnrIkCFIlCgRfv75ZyPey5YtqwI6DLHFNQeLczIquv1xoBvfPq+X59OVe5YIV15PVEALjKpAn2AOQmi4UU7KQGko9zsXOmFYsqCTU3TbaYnqhhucGUFgefoY011infwI+UNjrF+KYU41PVcENkeYUoRzMJ9tQaXrxDUR5ZHND5fRNtiZoL8R3Sk4oyDdSjgtNAd8/L4OGCjnlRE9aNW/HYl8qBWF0H+VUzbHihULX3wRAxXKvYs6td9DjWrv4acfY+KvP6PBy1Oa1YcO3JC/rVo48GOld0RMv4dfa72HKj++hwTx38OHH36I33//3Ygkb29vMz01Zy48dOgQtm/fbvxiFyxYgGnTpmHUqFHmtX3nzp3NBCINGjRAnTp18Msvv6By5cooXbo0ihQpYkK75c2bFwUKFEDhwoVRvHhxlCpVyoiu8uXLm9f/lSpVMjPk/fTTT6hatSqqVauGGjVqGBcCilem2rVrPzWxDMtXr17d7APFXZUqVcy+VKxY0WyL2yxZsiSKFSuGQoUKmagZTPzMfJbj9lnXX3/9ZY6Lxzdw4EBMmjTJ+JGXr1gBX3/6JepkqojzrdYa4Ywe0rA400NJEyp1R+YvUyPvV3kwrcU0nFxyEh57PXDr4i3cl556QChaHBYsWohsidPjdLOV+DNrFfzZoL5zSehAC/P69evNueH95eoGFDNmTDPDJc9tVIzCERmhbrBDtDFaCMPycQbHllutWV4jc3g25dlQAR0E+v5+MwFIP/PJSUIIfyxt5MfBaBN83UMrMWMf00UjJBhEnNMlR+aZ4Sj8KYw50pmDB+3QbSbUkDQaHBVth27j4EfTK1d3CiWKEBAQYPxTr1+/bgYDHjlyBHv37sG4ceOROXN2fPO1Ay2bO3D1kjSnAZIeuKRABzwkv1sXB3Lk+Bo1a9TBoEGDMX78OEyfPt2I5HXr1mH37t1mGmiGOvPw8DDW2Hv37r1yK2dE5f79++b4R4wagawJ0+F6O2l4e5/CwYYLsKrWONzttAfofx59i7dAindSoHfcXhgcbxAGxhuAgXGtNCB2f/T/ph/6fdUX/b/th6FJhmB0ulGYlG8S5laag2V/LcWWPltwYtEJXDt8Dbcv30avrr0QP0E8JEyQAIUy5EbpbIVRLHNB+ZwHuZNkwp6/3IA+p3Gr407UzlQBOVNkluUFUCLrD5IKIWXi5Pjq669NZ4KdomfBzc3NWJldBXNwiSHwtm3bZqKQKBEbGoc4aH3SMctwxChOpeR5yclG+JxkyD6Gf1UiN9LCK65QLNZfLydmiDVBhyscZEfLKWdcYtSLe5HcgspxMCb+phwL/auNMHb2pM18+CuAVvLcYixGRuJgh0JfVymRDb76ZrgwilJObrJx40bMnDnTWDtpTaY1l1ZcWnBpyaX1lFZVWnq7deuGsWPHGusfo2wcPnzYiFz6rFJYk2vXriNf/jwYO5rNqQMP/R24dsWBAD/ru/scB7JkSSvrqfB5Hnbt2YU0iVOgefZaKPJ9blQoXx6btmzChYsX0KVbV2RLlQkNs/2CQgmyoVqx6jjpfgLbB23HqhYrMb/6PEwpNAWj0ow0wnlwgkEYEKc/BnwrolrENP/yOwX3oPgDMSjeQPN9UJyBGJJgMFp/2xr53s+LTF+nwoCSrXCn0+5/WcDR8xgCux/GitpjUTJlfuOfvHLNSgTKv+eF1mfel0WLFsWbb74ZrICOFi0a3or+JlIlT2migSiRE1qlT94C5solZIQICmtGjKBRavghy+CmIfkiByqgoyD8gV71saJvuJ0COosw5pTQdKNgTGMOaGS4n3FHgA0ijOl3rT9YJaJDwXrjxg0zKI+WuNmzZ6NXr16oX7++cUkoV66ccVvg319//dW4BdBflOHkli1bhj179hgLMi3JtHCGBqznl6o18FsdBwb2cyBP7o/RsEFjrFq1Ds2btULOHP9Dz+4ONG7okP0qAx+fIIMrlBBhqLeOHTsawRwS9/39zcQqv/32Gw4fOezMfQoPAb9bfrh1/hYu77yM4wuPY8eQ7Vj+9zLMKDkd47ONw/DkwyxLduwB6PdtX2SImQGNc9cEep80VnC/LvuNeEa/c1j56zjEefdbtPmqDQbHHoRBCQdiZJoRGJd9LKYWm4J51dyl7uXY1H0TDkw5gLNr5P47eh23L96Gn7cfAkN4x3/6zGk0a94MX3755SMB/fl7n2BH/VkYWrKdEdp377qEUFKiBHTj5JTnnLOB8y9Uds5DQL/rbk6/68s6oUyEQQV0JIJ+2BzUsOqiFSOag+1KLbZGDdNizHjGnB6ar4joikI/aiX84TMyFKJeRSlocaNbBN0WKG6HDRuGtm3bGn9cvqqmvyxFAn0+KZDp90l/YPqIMgoCX+9HBGbMmGHC1w0fPlIETfD7RNE8efJUpEmTxli9lWeH57R1q9aYN2++Myds6darOyqk+gHrfp2EyimLIE/23OjUtBMqlqqE7AnSYVql3uhfsiVSxkqBnnF6YmCcAZZ12zXF7m+5lVCU2y4mLCf5XE6L+OA4g1Dns1/xjuMdfBTzQ+RLmh1lMxZGuaxF8UPq3MgeLx0WVBsG9DqJwO5H0KtoU+T+LjNKZCyAUhkLoVzmIsj8XVp89NFHSJUqlXlTokQ9bvnLs/2KNccD5zLILc9+CuzWW4EFZwEPfeaHKSqgwxlGpDhzy5q8ZOIxyzJcbaUVCJxxjH+Wz823WK927MF3kdmfOqpjuwC9M9waIEo4QxIHVCacCIw/YnWEohq0DtN39+DBg1i6dCkGDx6Mv//+2wwU46ttDiajlZhuEb1798asWbPMYDnbHSIq4OV1E507d8ePP1YJl2mmoxpzZrkjScZPkbOxA9lyZ8T58yFbol8FW7duNROd1KxVE/sOBBlV7uSq3PO9+/Q2Psyt2rRy5srvwS8Avjd8ceucN67uuYLTK05h/5T92NpvK1Y2WQH3X9wx9YcpxlI9MvVwDE4w0Fi8acXu+lUXlHyvJFLESoa/c1THieYM+0D3EXlAPHIfsdxJNtabhiqpi6FYgcKY6zbXuCsprycMnXvAy3K5ZDAExrrmoEb6YPNt80FZpm+aQxcV0K8AxlvmIIH50iMcID3FBnIzUxDnnwcUdEak4IQfQw8CK+SZwHB16lscvrBhOSQNDCdkoa+3bTHmPP2c1SraEODr8ZYwjjXCmmUyKBwwyrcBn48F3h5mdYT8XYIArLsk6w+1whReCjJANSJCKzFFMWd/ox8w/YUpgukrzEgPtBAzigL9hGkdplvFsw6ciir4+d3HwIHDkSZ1XPTq4TDuGqVLf41r13Y4SyjPi9f1GyhWpCRyNnCgn78DPW47kLykA3379HeWCHs4cO/cuXPOb2HEPaB9k/YokjAnfDrvNe4j6E4BLUK6z2mca74a6eIlR59+fTFv3jzj8sIIK/x98g0OBzLyNzt16lQzhXh4TTyjRAwYEpZjneh3zYnGcrkBv8gzipGx+MZaw8U+Pyqg/wO+fqfP0f7rwCJpPzmbUTMRv5yHnbGL+fqEU4b+sR7ouguYcdKK1sGbVXt74Q8bBU5+w4lpfpbr9NMymBiedpzv/vJcYnxuTtBCtxjO/Mj43Xb0K5ZlbHCG46OYHi7L35XyTTfhiTCDay5a4QnZGPnKdefkOJz5keufumWVoSjnRD2sj5PChMfENpwCmUJg8+bNmDhxItq1a2dCknEQHQUxBXLDhg2Nq8HixYuNiwVDrall6zEPHgRg7JhJyJY1BZo2duDKZTajkh468Hs9B+rXzy3fdcDgizBuzEQkyPg+Gu1wYICcz74ioAfIua0xx4EUGRJIxyTsZ3S8ddcbuQqkQKKPHCLsC+LM2bAR0jNmzUDORBmxuNoI1MtUGflz5MGAIYNQvGRxxPnwK3T9oSGmVOqFDEnT4PjJE861/g1DL7IjTBHN8QBt2rQxb4b4e+d4gT///NO4UG3YsAGXLl0yHWfl9YFXm64fay5ZMyVXX2W5hJaXZx7fnPJ5yDffDFOrPIkK6CDQclxvnWU1pp+R+xlrNryQJktRwh66RNCdhXE4bRhiL84EawpzWoL5OosDLyhWOZMjB1RygAY7NcbC7Fyvu3R63nBahSmmd3pYbjWubBIt9O14IP4k6TQttmaU/GSUFbWEQpvTuzPW9+djgHQzLLHNwR+cgp3Txp5x8VCghZvhD7PNsTpmoQEfePQJZgzh+fPnm4F1HFRVokQJ40/MgXX83revZaliuYjiQxxZCJDe0rx5i5EjRxrUquHAhTNO0WyHrROxx8gbxYs5pGNS21pJeWYunL+EPPnyoGB7B/rJOWWieGbqL59phU5VzoGuXbo71wg7lu6fihQJYuBIKwe8ezlQPqUDP1etBm9vZ8/4FcBZLb///nuULVcW23ZIr9uF1tK5jV2kCDK3a4+3P//MDDBkvO+XHRjLQYkMp8iOddOmTU28br5pYlSaZs2aYdy4cdi5c6eJZqMi+zVCLvVx0UUzRUhz3BVD8nFCGRoR+Yadc2hw7orXERXQSoSDYpghfdhx4ZSqnNimk8sb8YXSqaEbBV0lOFqZMD71u5LHmR1Jb1qOB1j+yDZ+0oNeeNYKzUchbNfJR8FZEbnzpY7G0kAkFKFMl40Wm62eOV91sW42FDa0IHO/ph93ZgSBYr2J1PXrGkvQ2/BVGYU+J+F5FugSsXfvXhNxgq4SnMiCDzaGW6O1uHHjxmbSCVqU+ZqZA/OU0GP58pUoVCgPqv/iwIG9TtEc6BTNrknyD+1zIG2aaDh4MPxcDSIbFGL9ew9Ewuxvo+VRy9psC2fXRGt0naUOpMuUCidOyJM8zAhEsx5/oGwaB/z6ynUeJGmoAyfaOJA7cQy0atPeWHjDkmELFuDrHDlR76onmsv3OmfPIVWt2sidNx/Wr11rFXoF2OMcKKJHjBhh3lTRgs3JcRj2kRPhMK45Q0WG9TlRwgc+O6+LeOZ4nwH7rTC4nDyOwQ3ohz3xqPUcp9ErKsKWX1EiDHs8LQHLgPM2Qw9YPsVF5Yfpcc8SvhS0ueZaPsl/yw+1qwjSaIOBXnusdehS8f5IIOkUSxzbMDLJQRHoWedYLhY7PKxGgO4ZtEwzTRVR/NkYq36+eWDkk99FiHO/6AedfKol8GnVfl7GHhPRffQBbnhdN2HV5syZgx49epiwa7QiURgz8kSLFi2MxYf+xxTGr+uEGuEFLc6dOjVAqpTR8GstB9asdOCOtzSXwYlnp4CeOc2B/Pnfg5fXFqsS5alQCKdOnQbZ/3Kg+00Hevv+2/pskpxf5vWS5akrREPnTl2dNbx6TnscQq4yqTGgjFxjEc4Y6JLk+/r6DqRP9BFGjRkvnWa2JK+elfv24dvMmVFt3wE0le+NA6WzLn+bSSorHb54efKidq1aOHf2KTN8vSLoIsYIIIyz3rx5c9OmcVZMzlRJH22+IaNbmHb0Xw9oSOLzc+l5oPtuy8D1gzzHOQ6MhqxpJ6yBj5F1VmJpBRTl1UIRyuDwByT9V090sPRiaf2tLQLVdWAlf2SJRMB+NAqIPcH6fEV+mPRNTzJZbuQBwAeybJn8UG044U3mWbJsIJByGtBARHljEdtZZltuG6mnW0KbLhucWbL6SuBP54jlF3WvoL8wX4PSYty+fXszVTLdKPgQ4bTHbdtwUM8U7N+/31hz+MBRIh70+fb33yafGkpKhkGD30CypA6cPSlN5kNJFNIi6qwm1Ert2jjkGseXzo7clMp/cu7+dnT3jo8GlxyovcOBAr0d+CiOAw03OzBQzmc/Ec4/T3QgZWkHcotQLdPXgZzyN3b8L6VTecVZy6tl5e65SJzsE5xoLdd4sCRXAW0nyZ/ykwPpvo+LpctXOdd8dew7cQIJ8+ZFmcVLjWimgHZNFNUN/fyRd9gIxMuQEX2kgx5RBhDSdYxjMBYtWmTaRwpruolwDAbjtjMsJGf6VAv26wH9qvmGls9hjiFj1LGC86wIInyDS4HNZ3xEFdjy61dedyhUGTuawpLitF+QGRifhpevJTjZs8zpZvUs6YLBwZeMTckBenTDcD9tDcCj+0JcSZtCeP6tvQR8Oc4qY4eBs+GsibXk+USxXGnZ44F+HIxHwU3/Z3vAXlDoo0VfZE4z/iKDIdjwcxIODrShywRdJypWrGgsxvQxZni2UaNGYe3atWYgjgrjqAEHDLZo3gHlykTHzevSXIp4fijiuVULTs3tQI0aDuTL68DfDRzIldOBHj3Kylp67Z+Vhw+loxLog3u4ijbdmiBlOQd6+1iuHG2lsxIvu4jrlbHQDx+hM95Gm/sOdPb5GIc8XF5RvTIC0bjb7yiW1gEfEffGfSM4AT1EkojoWz3lfkgnQjptBmNlfVWcvn4NaaXNKTBilHHhCCqgTXpoCWmmMouW4L0ECVFeRConIorIsN2k/zfDXNKCzYGObGMZ7YcDm+mqduXKFX0j95rAZzwneqOrJgfkU0twpmS6iDBww6hDwEbREhTh4RFFRH75yusOXRboClFTRChvVNtnd6aI6vgTrUFzHET34UignAhkilC+rGRkC0553mqLNWiP2G8x10qP8rOxwHsjgMSTgZTTrUgXNUUA84ew+ynRzujP/NYwy4XCdaCgDWNm07ocWly7ds1YjWn94GQeDP+UO3du03jT55iD8lasWGEENGMWa0SK14Pr171QsGAhdP6HzaSVPK84UKigA506x5CH+F+SOMFHdbnvv8XNmw7paHXmqspzcv2aF3LkyYyfp1nimanCMAeSFI6B/TcXWYWkbRG9bXxxw2IQm+ftiyhYJTX6lnDAf4AD59s5sOZ3Bw62lHvBKZyPt3Eg9v8cSPunAz9tdKDBVQdG3s0Db/9XF4Xllhx/sZ9/Rqa27S0B7RTLxhrt/Fzz6DG899VX+P6PP1BJ2q26IjhHyTm7QteJMHI1eRVwACNjzY8ePRp169Y1/te0YP8hxzl+/Hjs27dPw/W9RvBW5lvtY96PQ/RVXGZNMEMrdjP5Pk30Dd0tX8X8GSqgIwm0vo49bDnop54BpJhm+QaH1BYym/68jG3MnhmjT9BS3HKzFWWEESVSSR20CtN14QsRuxTKnJ/fNQoFLbodt1vRJJJNsfyM2fvjVOG/rZUbSL4PCTLHAC28tGp33mkJ4cyzgb57JO219j+bfKev89PgzU5hzn3kQL0XmXyEDemZM2fM7HVscP/66y/jX0yLBn3zONEH4xuvW7fOWI19fXWaZcVi9559SJ8+Aea7PRbPh/bTuujA3Dnvy70yUcSzKWrg71B0jfKCTJk0DckKvIV/LjnQ/6EDve46kDCfCNKR+eGH8HGJOXh5HfJ3fhOZ2zpQyt2B34468MuG6EiS3IEdjSwBzdReOlTlfyqHW/du4GEYGEbZfa8nHf1EFSuh1Fw3pKz9K77KkQPvx42LckuXGSFNEV1p42Z8nTo11mzcyNWiPHT7OH36tJnane4hnMCJ7nN0E+nevTvWrFlj3EdCaxp/JXJA/UMttPy8FTWk9horDraZqG6FpW/cTgH7RSt5igR4njk5VECHMXzQciAbBfGzwpkKv59qDWDb6/IsoYM+oX9QaRG1tBa7uj0wVjH9f0ccsr7TpYLuDw2DefvZRwQuxXBnl2gXjGnMMHBtZD1CYZzR6VM8WurkjTlQbkgKb4Zxo3vGN/KZfscM7Wbj5WfN70/Lte8LiIyg2pkWqOvXrxurMSfwYCxjTiDAyQMojGmZ6NOnD5YvX26mfb5165ac9xdQ4Mprydixk5EtS0ycOvZYPI8d5UCmjA7pkH0v99/mEDuuyvPj5+uH8hXLoUhXy/I8SFLNOXTfiIFVl4ZIifA52bf9PXDu4WbceHgGfg+lAZPdOBg4CwX7vIXiKR14OEDujcEOeHZxIH/StzBpynTnmq+eyZcvo8T27ah286axQg+X1NrLC1/nyYu8ffqhiewrRXTdy1cQJ2MmjBs9mqu91vDtIf2rJ0+ebFzwGOaTk84wxCfd8tR6/fpiz/exw9MyNHLSs2dBBfQrgk0+B88dvfGk9ZRxhzlIjtZVwtBq9M992qQrXH3ZOSCttM+06P5vrGXVbbTxsSvDlGNyMUUAcxCcvTkO2kswCUgzw7LonhYhztBvaeU7fZddoZ8RB+N9IyKdESkI94lRLdLPtCJPVFtlzcPP1yGMXhHaPkcUud7e3kb0rly50vi81alTx4RKojsFfY450GTSpEkmOgWnS1ZfYyW0oL9z/fqNUKWyA/duS9NIf+cHDjT8yyEdNIc8gAvJPfoCoVeUp7J+3SYkzPAB2hy3Bg/28nEgdXkHKndOieuBr86X+EW4H3gPU67VQKICDoysIPeI0wq9oLYD2TKmkjbpGZ+8L8nt+/fh4eNjjAl2b+6u5A25cQPxKlVC+kZ/m8gcTH9c80KCEiXRuWNHU075N/Sp5ttKhuGzrdd8U1m9enXzHNounRUabdQQo7iiAvoVwJ/YMRHOHNRGH2DO7MPg44xfzLjCnGzjLRHRdJvgbD+cTpMW3M/GWIPongX6BhuLstRTZzVwVXpPHL365lDLOsyoF61FpDOUG4U1o1sQWpO5T+xlBYWD8dgTexXw9Rp9jTndM8OzMUwb3SloAWBjxdmw2FCtWrVKwxwpYY6HxzUUKJAPvbqLaGaUDWkaPS87UCCfA927R5fvrSU9x2sj5ZmgIKlT6w/kaiTiWc47LdB/rXMgdlYHxm6mM0LE43LgHjRamxTJ4ztwnNE5REAHDnLgjxzR8Hv9xs5S4YOfCMHZIqTTtWyJxOXKof7NW8YS3TgwEKl++x3Vq1ZVo8MLwIhJdPXr3bu3ib/Pt50VKlRA165djbFHxfXryWstoOlSsOisZRW2o0hwwNtno4EuQSa68JY2h7MUHvSyYhHbcGKMPO5AhpnWut9NscKv0PLMQXYxhgF1Gdve5bdlXCMGWgLYhq4XX4qgzjk3ZGf3bR6WL3LhBdbkHp+K4KZ1mYPqCH13tkuZSUeBuacs1w/bzeNVwUaDods4u527u7sJps/QbQxLxOgUNWrUMHmMC8qpZNkQGauJokQQNm7chnTpvsXKpZZwZtq6yYH06RxYsuRTBAZKT1h5JRw+eATJM8RFw22WeGbc5zxNHMhR60tc8JOGOYKy/s4AZGv+FupmEfFMVw4R0WfbO5D1uw+xfOUaZ6nw4aG0r+tESOccMgRfZs2GP695PRLRWbv3QIGChSJ8NI7IBJ9/W7duNZPLMJ4/35basze6ubkZy7Z2WqImr7WA3nwFZjINDsijj25w0L+4rQhdTuwx5TjQb59lOeaAOq5Dqy2ntXxvpDW9tCv0dc4jQpdTN2938U1mlAvGJaY7hR12jeFa/lgHvCGCm4MFQ4LuIE9z9whNONjiwoULxpeY00D//vvvZlAGe9+0Gjdq1AjDhw83g/TOnz+vPXAl0jF06CjkyPY2LpyVptBpeR4x1IHs2UQQnU0l97RzZh7llfBPhy5IXzUaet2zBDRD132b2YE+S2ohABF3UK9PoBcGnSiBBNkdcK8p980wS0TTreOHgvlw65bL7E3hgYhleVThx9Wr8UmKlPh5xy4jomnTLzZrDlKlTYfjx46xpPIK4ZvXAwcOGLdDPj/tqCH169c3vtgU12pQiry81gKag+I41XL0IUDciVaoNopa+vxecApqSkKGVaM7Bme1Y5gUTg8dYyhQ12lo4AjON6QOhmgLOoKT4drS02VjuCW8GZqNPsb0aaaFeq+LSyWtxWEhQTmojoMplixZYkK0sddMd4pixYqZwXhNmzY1wpjuFBzVzMEXihKV8PX1Q61a9VCrhgM+It7YFPr5OFC7lgM1RRBdv14Rfn4eVmHllXD1ylVkyZUG1WZb4pn+zyV7OZCmxGfYf4vhASM2J/1Xo+asOMiSyAGPLpaAvt/HgQppHOjSraezVPhCu82vO3fi0wwZUHbBIiOg6RfNCB0J0qV7pVN/K0+HVmmO96GVunXr1masD5/BfGs7aNAg7Nixw4wJUiIur7WAJnR/+HwMkNvNGswXFB9/oPIya+BfcxHP9B1mKDb6EXNAX4/dVhxCiupqK0O2ZIcF9Bs+evSomQWP00MzhjF7vHny5DE/TMbKHDp0qIlpTMuyoryOXL3qiSxZ0mMQX72bJtCBS+cdyJlDRNygt3D/ficzqEh5tUwYNwnfFXKgq5cloDt7WBOnNJ1QFHcC/iPOZQSAlsPVfh2RqmY0tM4t9xEnWhnqwN5mDmRK/g2274wYby+uy352uXoVX+TMhbx9+z2yRP96/iK+zZgJE8eONeWUiAX9qvn2959//jHRpXLmzGkG0tPvmm99aQhTwpfXXkDT64ATiNAnOckUKxTcByOBj0ZbFmkG4SYctHfkhhWt4nniBL4sDKvDmZk4UIHit2HDhsZKTP9i/qhoPe7YsSOmTJmCnTt3ajxjRXkKy5evQdq0XxofZ1s8r1puxXdev/4rBAa6mzZBebXcvXMPRYoURjkRnAxbRwFdZZwDSQq8g+UnRjhLRXxuBVxEz0M5kSC1A5sbyP00RNJgB3oUc6Bc+QoRxvfVLzAQg0REJ5BnR7oGDdFU7nEToeOGNxKUKIF/2re3CiqRAvpdMzLIgAEDHvld063S9rumZVtdQ149r72AJvRjphU5LOAsdpwW+tSpU0YUc+BBmzZt8PPPP5uwOYULF37kXzxs2DDTA1U/KUV5eXr37o/cuRy4evGxeO7d04F8+Ry4eDETHjw4asopr57FC5YhUeb30cnDgf6BDnS/6UDK8g781Ckjbj6IRG/HRIge8HVHsf6foGgqB+5xym8R0d49HMgd34EJk6Y6C4Y//vIMcbt/H+lbtkLCEiXx16071uDCgECkrPeHidBxXwe7RXqoMfgmesKECSa6FcctMfENNCNgcSZHNbKFDiqgQwEOFKBLBEO0MdpEt27dTHB2hrmhIGZECrpTcJpo3sCMYczy+gpGUV499OGvXPkX/PWHNHcBkh5acZ5/quLAn/Ud8PP7RX7D6msYVtAY8MvPNVCwgyWeaX2ut8KBuNmiwe1INwSaufYiD/4BfpjtVR/JSkdD3+KWgKYrx8rfHcic9jucOn3WWTL8eSjiapU8d/INHYqvc+TEb5euGBFNa3SWbj2Qv2BBjdARhaFrGudPYLxrGu6oUejmWVU6T/379zezNTJSlvJsqIAOAiNJ3L1711iIN2zYgOnTp6Nnz55o0KCB8T/i7EX0J2aYGk4N3a9fP8yfP9/MYsR5+tn7UxQlYnD27AVkyZwM40azqbPS2ZMibDI5MGbMW/K9HwMWKGHIvj37kTDth2iyyxLP/aVTk+03B4r+mQznfIPED40kXAs4jhZbUiNZUgcONZf7bLAlohvlcqBuvfrGyBJhkBt+r48PqixZgk9Tp8FP23a4ROiYjTQZM+LI4aeEglKiLDQ2bNy40czJwElkKK5pAOQEZpz1l8EH+AZdsVABHQSK58PSeDAsGwWxDiZSlMiJm9sCpEn9KQ7ueyye57s5kC6dA7v3fCvfV7GYEsY0a9YCGWs60NvXEtAtDjjwVepoGLTqD/g/jKSvlgOAHb7jkfOft/FzegcCnNN8X+gonYPE72LegsXOghGEhw9xRkR0/d278UmGDCjtPs8IaKbKm7cibpo0WKcROhQX7LC2ixYtMlFD7InQqlSpgu7duxuXVI7Bep1QAa0oSpSCU3J36tQdRYs44HnFEs4PAx3o2smBQoUc0sjnkDLnrMJKmHLqxBmkzZoUdZdZYesGPHQgfwsHsv78BQ7fWeEsFTnxeXAH46/+hNjZHZhVTe67oZKGODC1qgM5s6SDd3jHhg4GOmt08fDAV/nyIU/ffmgS+NBYo389dwFxs2XHBI3QoTwjNDhyYCPHbtWsWdO4rzLQAWNej5X7iMs8PT2j1Ft6FdCKokQZ7ty5ixIlSqJFM2naODGKpJvXHShTyoHmzd9EQMAfknTsQXjRr/dAfF8kOvrLdaH/c7vTDsTN5UCHOeXh//Cus1Qk5SHjLu9CnYVxkDGpAxfay/03WDpvgxzGKt2ybUfjIhjRuC/7NPrePcRjhI6/GoiIDjQ+0X/evIXYRYqgU4cOVkFFeUEomimw9+7da6KJcYwY3UM4KRs/c94JjiFjdJHIhApoRVGiBAcPHkbmzN9j5nQ2a5Z4PnnUgUwZHZgyJZY04kPU3zkcuXbtGnLnzo2fp1quG0wVhjmQvHhMbPOcIU9ZZ8HIjOjjDQG9ke73aGiSW8TzQEtEn2jtQMZkX2PDxs3OghELynp3SWmbN0PisuVMhA6K6CYirlPW/Q21qldX31fllUGBfeXKFaxdu9aMK+OgRkYOYUQyhu6dOHGimVjm6tWrEWo8gQpoRVEiPdOmzUL2rO/h6CGneJY0Q4RahvQOHDqUBL6+azW+czgzd/Y8xM8eHf9cssRzt5sOJCvuQL2BeXHjftSZ2OkB7qHP8fz4Jo0D6/6Ue5HTfIuI7lvSgRLFisDvfgQaUBiEDfIjyc8IHTlzoe6ly1aEDsnL1q078hUsCO+bN62CihKGMHIPO+C0YDM8X+PGjU0gh7x586JSpUpmspk5c+bg+PHjYTpzsgpoRVEiNQ8e+MHN7ScTlq7wDw706uFA3V8dKFfOIY1uXtz311k3w5uHgQ9RtEhRZKjuQJtjDvTwdqD2PAe+zRAD8472dpaKOpzBapQb+SnyJnPgbk9LQHvL3+IpHBg8NGJPFHNA0o+LF+PzDBnx887dRkQzMUJH2kyZNEKHEiFhAAgK6CVLlphBjbRi2xPM1KtXD6NGjTIhhBnGj7M2hwYqoBVFidTcv39TGsTB8PPLLt/ehb+/A9evO0RYN5YUyf1qowi+fj6Yc78GGotw/vO4A9U3OFBmmgOtdibFZZ+oJ8gePgzE0gfN8X3pN9CrqDxmOc23iOgdfzuQPlVSHDh4yFkyYnIuMNBE6Pg4dRqUXbQETQMCUOPQYXz340+IGz+B/L6uOUsqSuSBMc4ZcpjWas7gbLuKcMBj3bp10bdvXzN5HQc7PgsqoBVFiTLQTcPf30PE9Hl12YhAcPCct98VnL69A4d8F2DD7YGY69EEe27NjlKj8l258eA82mzLjKTfO7CnqTxqGZVDRHSr/A5Uq1lbOncRO0Sqp+xfl8uXkeLvv5GxWzeUO3gQtST/T0k7fXzwUGfHVaIgHOz4rG4gKqAVRVEU5RWw13c68nf6ABUzOBDYXx63Qxy41MmBLHEdWLBoqbNUxMVXRPQMEcsD7t3DGhEVniqcFeURKqAVJYLBHjBnfipTqiQqli+rKQqn0nKN//yz/ms3AcHrgv/De5jq+SuSFIiGcRUtAc00t4YDubJlwqXLV5wlX4zdu3fj56o/o1yZUsHeX6GVKgWTpynkVKZUCXTs2AF37txxXiklKqICWlEiGKfPnEW2TOnRoUpqzG9fEHNa59cUBZN72wIYUCcT0qVMgp27djuv/mPu+fggUfx4yJTwA1TJFQeVc8bWFM7pR0mlMn6JTz94B3PmzHVeqadz2X8/Gi5PjjQJHDjV1imiBztQO2s0NG7Wyri3vChTpk5HpqTfYOLfOeHWpkCw95lbq7yY1yI35rV0SfKd+XaZua3zSX4euEtyXZf5zHtiffnMvLnOMqZ+yXdrle/JdeW7lZ/XlDX12HUEk6w6n6zDta7glrNu1315nG9t+9F+m79SLsg+/uvcyOfn298nt8s0r10BtKucEpkyZzFh15SoiwpoRYlg2AK6beVUcBORNbNlvkdpRvP8mNU6L1YNTY99ixPi+IZvcUzSbvckWNI3M2ZJ48+0flwqHFkdFydk2cnN3+Do2jjYPjMZFnbLZuqw65sun5f0yYI98xKbsqxvzzypS/JmtpAyklh+9bB0OLHpW2ycmPLR+vy7VLZ5bG1sbJ+VzOzXgq7ZsW9RQiwbkAnTmznLtZAHYPtcOLgsAQ4sjS+fc2N2mzzYOec7HFsXGyc3fYMTG7/FgSUJzXZmt8n7xD66JuYv7p0Fx9fHxqmtX+OUHBvXNccp9ZzaLHmSf2BJAszrnAM7ZiXF0XVxcHLjN2b5oRXxsXF8SrMPM3h8rnXL9/VjUst5SmqOxRx/kOUz5dyuGJQB+xcnMPXxfHFbq4akN/u2dmQasy8bxqU260xvVgALumXH4ZXx5HrEwaKej88/H7Z9a2cMWUDf80Hq5N+hebkUpqzrvgSXZkmaJMfVc2Am9JfrN12OgXlBy4yQa9RtcAZ0ldRlyOPUVdKIrjnMen3lunYbnNHkuZbpNiQjRnbJgb79MqPLUOd6Uo8p61Jf90EZMVH2JbjtT5frO0Cu4bh/csp367j4d0KHXGa/p8q98Tg/H+bK+Zra1lqH+91b7q3xHXNJfgHMlnvLLjdHyo2T/F4DMppyg3plxTTZFtftJeuEuL+Sz/2d3O7xdkNKs0SAjW2YA6kSfIE5c92cV+o/EH280XsYMjZ4C3/mcMaGFhF9lLGhE8bCho1bnAWfHwrojCKgx8k+zW715L7PaiG/I8nLt22hedB/5O2FOJdO4dMbnnhHOmcZD26Sc/QT3JrmkHPwO9729UHCs4flHJbE3GY55XoUx49LR+GL65cR684tfH31HL70vCjlfJHh4Ea5D8phhpyvIutnwyHHWGPeAMxuznMoAlTWbzi5o9lujl3LMaR7ZWQ8sBFxrpxGXNmHWHdvm2Uf3rppvse5cgZpj2xDv77V5DrmfuI45jTLhT9mdDP712jKP6Zu5k9uWxiZ9q9H/AvH5b6tINuWdkW2z/3Kt3Wh2cZn16/gW6n7w1s38NEtL5RcN13uy2JSRy5z7Fn2r8N79+7gK88L+FzKvu17D3Vn95J7rSrSyP5wv+JcOo13pQz392Pv6879PY30h7ZgeNeKZpuu+zu3TX60qZhCBfRrAO8JRVEiECEJaIq6M9u/lBIOnNv9Pyztl8mI5Tlt82CdCL/1TtE2SwTICRGMeODALrckmNa0ANxFrJzeJus+dBgxR3G7UkTfvetv467HO2b9mSIOuI0NIr59b7yF+7ffxEoRGVObFMSuuUnMdo+IELeFMf+uH5sKAT7RcWHvF0YUU1DfkfpY1uPYx1gioofbp5i94xETt67ExLxOOYyA9Tr9gdnOioEZTF2Le2XB2Z3/AwIdOC6i2IhY57G7JgpZCtNpsl8sw3Px4O4bRvxOa1wQ02V705oUwMIeWeF1RrZx8y1zHNNkHZ6zG+dimX3mcbIDYeqUv5snpcCDe9HN9g8uj2fE8qPtyrnZMz+xOafXZb957mY4ly3sng1z24kgb54PexckBPy5fnxzHVgPv/O43ETcuXYMQltAU0B2keN8/8abSHzyA4ylQHUKTNcy5ZfFF8HjQN6tX6HNqDRoJeeNqeXY1Bgs52zMPzkQ5/x7iHn7DdSe+x1aj7bKcDn/skwXOf6Wcu1bj06N/Fu+hkOOMeuu/5k8lmG94zo+Fsh2mivXoP2ItIjm50CKIx8ZwT9b9mmKnKtccn86JL/hlORSLr/J7yQdxS/lnvno+luoJJ2v5tL5qTs7KeKfeR+O+w6Tx2MaIPfOx1LmQ68YqDP7OzSWa1lg09eouiCREfIdh6dDC7ne3Lfsci24v3nk+Ln/PK62sr8TpZM3K0inKWh6IQEt+D28hYGHyuDbjA6s/E0eu04r9LByDhTImwt+fn7Oks/HswnoReZBX292TyxumFE6HXlQevVkk1du5UQjJrsN/s2I5O9O7cekdkWlQ1EX78t3iue+fatjXpPsRti6Nc1pPrvze7PcmNa6IIqvnYE3/B/g1zm9Tb5bsxyY3zgLmk5og2gPApFr5zLZH2mnnALXvUk2lF01yWy/+vzBcJN1mG/Et+wzy1KE28cwpe0PSHl8pyn/9dWzIrKrY67sRy33/ogeEIjoso3fZvU0HYFOw+oj1m1vJDx3FCO6VTDlKKy5X21H/m2OKeH5oxgmy2rO42TyEGG/HqM6lzFlmGxBzPNE8T5LvhfZMAeOQOCPmd2kzlzW/spy1/NtJxXQrw+8fxRFiUAEJ6ApvPYuFHEW4MCx9bGNcKZllwJyab/MRiDSMrqgWzYjZI9TQEtZzxMfGSvveRG4FMTXTn5oylPcXT38iSmzTgQSBan9AKCo3DotGQJFoJzf87nZ1s45zyGgPd8RofwuLh341NR/6cBnsn/pcVvyghPQXMZt8hgpMq8c+sTUuXFCChHf+Y0At5PrfvL454hwPb/nCyOgN45P9Uig8i8F9DXZRoDvG6YMrdYexz82ZU9u/tp0KmZKOQrudWPSiHh+w3Q8eKwP5dj3LUxk6rGOM7Ws9yauHv0YbrKevR3XZAvoh/ejGZFN4R7oF81Y7bnvQcu/KgFNEfndiQ9DFNAVRHQ6pCOQ7PhHKLE6DorJ/VF5cQIM70ZRlN8I6HjSyXhbzlMu6bAVX2OVqT4vMSYEsSpT5Fabn8gI4rIr4olgE/HjFKHcFuszST4zf7oszyl1cvsUwBVlX9zl3Pw2Myne8I1m8tPKfUPRSyv4p9fexv/knhkq9zXrMNuUY5oo1z3rri/whk801J/6PUZ3yimdhg+NMM6093MjjKe2ziOi6snzzn0ovyye2d+f5Vpx/12X/1d6UQFNzgSuQ42pCZHrOweudpJHrwjogAEOlEoVHd179XOWej6exwJNC+vnXlfMZ1qiKZopaimEuw6pZwR0UhHQE9oXM8KWVuVi62eZOigWx7cvjjRHt+M9nzv48PYNlFo91ViBS66ZZsTlJzevIe6lk8ZCG+/iSdnWVbOtPNuXyP7wvrBEMS3IZZwCvtqCIUakUpD26VsDpdZMRbENs0yqN6uHEcAtx7UwAj3PjiVIdO4wcuxeiX+G/YXPvDyQf+tCxL58BklP7zf7V8utv9mXglvmG+u4fS54nMO7VkACEc+0Rv8z/C9T96jO5VB14TDEv3AM0QIeyn6fkE5ay0fi2JxD+Vt441xT7++yT7bADimpgH594D2sKEoEIjgBTRG3ZUpyPBSBcOngp3DrkMuIydkioFcNzWDcBmhdPrbuW0tAb3BaoOcmMdbfq8c+FlH6hnFPMAJYhMxppzV7x+zvHgs8ERgUh4dEZLC+oyKwuMxVQNtlKW6DE9B3RfRcO/UB5rbLZayzniLUWBeT98V3gxfQsk88nmX9MxqL+N1r72BJ78xYJCL47I4vcXH/57h44HMcXBbf1Evx/CwC2rZAs3Oxamg68/nO1ZiWi4mUYblVw9LBzzsGfGRfdotI3D4jGW6cfV/OdTRz/rhfdJnh8psX38OiXllNnuv5MvtDAS1ikp0GWuG3irDjvvH74VVxzbViObOepHAV0IEO/CL7SoFJUWmLXopTCui4IqBp0aWInSPH6lrGNQUnoLkNuol8e+E9vHUvuklxpL6RXbKjk1yD92/EQO5tX+K3GUnxmcfb+FHE+1eX3hURHx9ll8fDW3ejo/m4VOjTL5Psw9v46nJMEffSMZR67W1SYGcTAf2m3Ht/TvvebJNWa1q8u8r9lG/LV3hDOi+xZR/69slsjovrhqeA9vcLwMrbPZCqajS0Lyi/B8aGHmqFuEufPC5279nnLPnsPI8Fus7cPljUKJMRiO+KCKZrA63L7k2zPxLQtEBP7FBMrlV5JDh3FG+KcK3t1s9YmmmpXijrN5jayYjrAiJSKaBLrJ1uWaClflqo5zbPhXlNsqHJxLZPWKCfJqBd99lOFKq0hmfevx4feV9HlyF/oH+fX/DNlXOIFvgQebcvwtQ2hVB+xXhEfxCAhlM6GpeK2JdPG0tzi3EtTeeA25vUvgiKr5sp9/1DFNrkbqzak9sVxuCeP2F66wJY+Hdm6YSVMeeErh/9+1iuJOYcyn6pgFaCg/ewoigRiJBcOCj41o5KC+9L7xm3gGsnP8Lx9fRx/toITgo1+hhTyJ7Y+LVxRdgj4sYIPBF3dOegddRDBC0t1RSxXD9Q6rp5IZb5fGb7V/ARkUlr9d4FiY3rArdLP15ahinKacU9uiaOEbWBvtHN/lBgUljTReKe11u4fuZ9uHXMaQQj118xOCNui3CleH0soN9HoOzP2Z1f4vi62LhxTkSrfKfFelHPrGa/zbFTuNnJeS6YbAF9Yd/nTov1vwU06/S7FQOrhqcz+8fyp7d99ahzsGqYJYx9RKjR/5pW6Xmdcsq62Uyng+eQnQ6uu1xEN+vjefY8+aHxrWZdPl5v4/zuL8xr533OtwSHRUxyPyi0Kewp8O9JudWyH/Y+vkoBHed8LLQfmdb4Q/cYmNH4+A6Uc0rrsS2gi8o5793fuVwS/479J5flwiGC9yO5jn36ifi0r0MwyRbQtCYHtUDTXYMCnYlWZvo2F9z4zSOBzHyKZu4L3UlYF/cjlnRmMuz7TMRZHmNdfvtOdMQ+/5753FU6Qo0npkBi6aBFk21WXpTArEef6GJrYqOq7EsXEdB0IWEZuqHQZYTnhvtkC2jub1gLaHLrvie6782Lr5LLb5WxoenKMdCBf37gzJllnaWenWcR0BWXj0O8Syfx95QORgTTujr2n1LGepvg/HEjdCmkvz+5B3m2L8aE9sWd4jGP3B+1UHz9TGOZplU58dnDyHBwE35eNFzEZxVT/y/zhxiXiUZSP8UlfwdzRES3HdVY6j9m3ERcBTSX1Zw3wOxT/eldZJ0nfZ7txLq6DvkdyU/sRqm104xY5/63Gd0EhTa7O321c8k9WtOUocilMOa2aLXOvmeVcdegVTnF8V34cekYDO3xoxHVPAfdB/8mInyxHNMRxJVjSyF1/Lh0tHT+ypttcx9sAf3T4hGmnmYTWj9aFlJSAf36oAJaUSIYTxtEyGSstfLgNwMGW1uJ4pJizRZnXEaLJ//a69nWTwpsJjvPWKS5jrMu28f4X4PspG6mR9uVv/xur2+nR/vkksfEbbnuD8twwKDZT2d512N41mTq4foiboJbZup2WWbvB88B/ce5D8Gty8R67XPFxPNun3t7v63z5XLepT7X47TFvzlW2R5FGPNDW0BTHHIQXbuRadB8fGp52Kd6lJpOTGnENQcIDuyVBS3GpZYyj5fbaYh0OqZJmY7SmWj3DH7BXDZYhHlLqa9/7yzBlmFiuUnSeWk/Ip3xR+bgPlrH6fvcS0Q8faH5nS4eFMn0u6YopvClyB3eNbsRws1EePMvBzIy37awz5BzOqpzDvwzNJ0R5+2k88B1aHkOuv8cjEi/50HsUDzl2IJLLyugOaDwyIP5KNX/fyie0gHfPvIIHuyAVzcHCiR7C+MnTnEWfDaeJqDtRLFoW1ODy+dfS/RaPsquZZi4HvO53C7vujyk+vk9uPJMIa0TNAVXh9kf1+8h7Lu97uNl/96WqculjO17HTQ96/4yqYB+fVABrSgRjNOnzyBD2tSoWzghBtfLjP6/ZtIUBdOgupnRrEwyJP8uPnbs3OW8+o95XgGt6dWnlxbQgv+D+1jg2wSJ8zswpKwloOnKsb6+A2lSp5YO9Blnyf/mWQS0prBNKqBfH1RAK0oEg3Fhvby8cObsOU2vQfL09Aw2FnBIAppWWdstgm4SthWWn5ln+/vayY5o4ZrHgX3uTQqYuuw8WmPdXOpjMtuRciEmWc7yrJ/fXeuz67T30zXfNXF/7eNh4mfWE5x1mHn2cVr1/rsc13XdF7v+oOW43/a+cdl/HSuXz5b1XlZAk9sPr6DRuqTSeXLgeGt5DDtdOf7M7sBfDf5+5tjQwQloul3QLzjt4S3IcGgjKi4biwG9qqLHwLrIvG8dyq2chKltfpBjtqyvdJOgT/LozmWMpZV5A3v9jJy7V6DIhtkY809pk8fyzce3QunVU4xvMt0neg74FRkObDQuEimP7ZJtbkX6Q5uR+ugOpJS85Cf2oNj62cbXuPi6GcZlYnCPH812uK8c6Pfr3H5Id2SLiaBBK++T1yiv8b+uvGQ0Mh1Yb0LLsf7Cm+aiwbTOZmCgbRWmy8n4jiXQeHJ75JPtpD66Hdn3rERN9wEY2PNn69gk0deZbin0DacbCtfngEW6ukxqX8zUw/q4L00mtUM6OY8t5Lg7jmhotp/i+G6kOrbT5DOUXapjj4+1gpz3me1/EAGdXAX0a4AKaEVRlAiIq4DmhA10v/h5YSLj48wBfp95voOYd98wA+boL1xqVRzj21vDPbERjcb1oVt2xDsTC0XXxhZhYInLsR1zIsO+T/Gu95toMTaVyaOI/HtiCrx3603UnpvECGzGac605zP8zyOmiYTxwc0Ypv73ZD1+Z37C0++j26AMZh1HgANlVsQ127UESH7jnvH23ehIeeRjE+fZVZwzUQA3nJzc+DnTX/mLqzHxybW3zX4kP/oR/hmWzpRjnZ2HpDODI9/3joHPPd7Bp3L8LJfi6MemHLfHxGghjMZRelVczG9c0ITW4z6XlPPD88S6WI6uJO/LMWXZ/Tn698mM7499ZB2r7APr5bFyuTlWyeO2B/fKhgl/5XxpAU32+E9FtlZv4ZdM8himFVoSJ1rJluRdLFux2lnq6bgKaPfmuYxY5kO9zOqpRvTSJ5jCeUSX8sZfucyqyXjz/n0jWimAGTOZESy4Tsm10825ntK2sPEfjnnvnhmIR9cG43s8pqmJH82yFNeT2hc14pPr8C+3lWXfWhMnmiHs7MGBFK2M0xz//DF86uUh90QtOf+WUOY+/bDJ3dT592TLR5v5dmK9k6Xe70WcvuXnh85D/zD7M7xbRWQ8sMGsx8gb9GsuK8fmkI7HD5vc5B4vadaf3K6IEdAx5Jjp4zyqS1mzLn22GaKPHQBug50CDox840GA+UzRzrB49PVmPgc72vGneV7H/FMKSc4cNBE92AFxHQipFujXB95/iqIoSgTDVUC7tyyADiL4KOwYIYPCdJ6IQ1pGzUNdhCn9nylUP/R6yyynxZSxkDlIL4ZPNBE1KTGvSUFUF4FNgVllUQIjlCkmm4vIZKxlCsV3ZRt/2bGYnUJ8rtRVe7aI5AciTFfGlWWWhZfLWa6mm9QpApoD9Bb8XchsZ6H8pb/xfwlobiu6bzTk2/y1LM+HRY1+MIMXP7gRA7HPxzJxp8sttwb+MYa12aZsm8c3VQRxHsaPlmU8Lu6XfXyPBPSY1GbgIvcvxr3o+GlhQjMwjDGmKZAz7f3M+GcbAS77w30otTKOidRRa25iy/LsPNbQcOGw8cddTPL8BQmzODC7mjyKaYUe6sCEHx3Iny8vrl+/7iwZMq4Cem7LvBjVuSwKbF1gxO/7t71NBIzOIvAoCCk8J4mgTHN0m4jHK+jdrxaKrZthRG2OXSsQ6/YtI3z/mtYZb/j7o/LSMUYsUhy2H9kIH3p7mZB0zce3NiKZFlxGwaAAfRYBnfDcERPVg8KT4fBSH9th0qc3PIxI/S8B/eYDfyOG241qjPIrJ+Dde3fxxbXLcq/XRtfB9cz3xGcPmXNgW7jp08zPDH1HsfPHjO5mkGAi2RdXAc3weRTZDJUX+8oZ85miufLS0SqglRBRAa0oihIBCerCQQE3plNOEXVJjOX3Td/o+Oryu/hjejIz+I4CkFE1vvB4B1l2fYHac5IYMV1vZlLk2fol4pyNhcYioimUM+/53MRSpjjk4MKYIpopJDmor8Cmr8z3JlKWdTJyBwVkLamPAroUQ/JRTDoFA0WnEdAiYt++84aJ3mEnClSK2dSHQxbQDURAU9i+e/sNE7KO1mWKeFqEuw3KaCzmtP7GEBHceUh6s0/2+tyPejOSmXjQObf/z0T6qOEu+/mEBTq1iTFNS33T8SnxiRw/OyI5pDz/2gKawpmJkURoraaA5nG5bi80BTTxxAHUFUGfKZ4DlxgbWkS0fz/p3GSIjvadujlLhUxQFw6KQQo9Wk8pmhuLKKXlljPtDe9WweT361MNX3mcxwe3b5pwb42mdDTHVmTjXDPjHmf8oxCmm4ab1NVz4K8isj2NqCy6YTZ+WjwSic4eMeKhpAjwmc8ooF/WAs3tM4TegD6/YEiPKsa6zE4Bo3oM6vkTOEsiY1H3HFBbjtMSuzwXdE1hNI6YIrA7jmjgFNBPWqBLrZmGN+/7mxkPuS6jg/D8cL8Yvq7agsEqoJV/oQJaURQlAhKcD/ToThRGeY0wpLDLK8KYwrWuiGQKWVpgG09KaSZBocW1wtJ4kl/AWKeTiSDlDITxzr6Pgb2yGvHcY0BG/O/KO4gmgpOCl+KVsZcpHmN5v2miWbDOZxLQsr2yy+Oa7VEoc73e/f7bhcO2QNNaznXmNXnsl2yXq7IooTlOdgQYA5oWblrfOQNhIulM0MLMWQZ5TP924bAENEPl2WH2as/5Du/cedNY57NIZyK8BDTZeG8QUtaKhlb5LQHNxNjQGZN+ht17DzhLBc8TLhwtcqPpxLb4QERdvIvHjT9yggtHEevuLTPz39TWhSyLrAhAhq57R4QyfXbtPE7dneroDhGiF4wPNMV2n/41jChlbOSWY1sYf2hOPjKseyXk22rFl6brB2Mp0xqd/tAmuQ8eyj3Y7pGopIBmfOZvLp8xVnEKXFcBnd9ZT0MRxyEJ6MRnDhkh22nov/2kmebIsQ+QfU5zZDvelg5DggvHjKWd03zzOOmjzXB3rH9Ijx8R+9JpcGrvHgPrmG1wwhhamuvO6mX2m8J8eqsC+HHJKCOsf1o8XNZ9LKBHy3lg3TF97qHL0D8fHSuTCujXBxXQiqIoERBXAe0mD3NOTlJQROZnnm+L+HsDH4vgzbj3cxO2jg9uW9Dyb7ll8YxFlmKTopUisFf/jEh84gO0FVFM8UkRTUv2p1IfrdAUpbaA5QQqjL385eWYJjazm+TVnfmd8bkuv9xyo3AV0HVmJ0HMe2+YmQUptk2+/KUrxoc3YiD9/k9DFNCNJlm+14U2fGM6B3a9rml283wmjnXh9d+afeLx07pNK3Wd2UkxvgPDkFnbpD92TFleQfaTApoh8WKx/o3fGEs9RTLL0h+aQpmzLQYV0HQZeffWG+a4XrWA9oMX+u4vgYRpHNjSQB7JQyUNdqBrYemQlC0Lf39/Z8l/QwGdKdk3mPh3Tri1KSD3SV64t8wtKS/cJLm3zGPS3NZybqQTZif61HP5XDke13w3+c78J/KcdbnmmXxTNo/565rnLvsQdHvWMqnHLAuab20zuHXsZB3Xv9cNmsz2zTG7Hn9uk/9kuSf3heeBx/Lv82TVF/Q8MZk6gjkv89oVQLvKKVVAvwaogFYURYmAUECnSJoIjUsnw4zmeTC1aW5MY2rikuQ784MmUy5InsmXdYJ+D5oX0rJH23Z+d03Mmx7SshDy7fS0eoOmR2XtFGT5E2VC+P6vskHyHuUHs860Zrkx8s+sSB73U8yaPcd5pV6eUw9Xo+Lw2CiUxAHvHvJYHuLA3V4O/JA8BoaNHOMs9W9WrFyJTBnTI2fGFMiXNbWmCJIypf4OVatWxc2bN51XSomKqIBWFEWJgDCU2e7du7Fo8WJJSzRFkLRw0WKsWbMGt2/fdl6pl+eh/Fvk1Q5JSjnQv6QloDHMgdV/OJA5bVKcOHnaWVJRlIiCCmhFURRFCWfu4Cqar86EJN87cNIZGzpwgANN8zhQ+9ffnKUURYkoqIBWFEVRlAjAkQezUbDt5/gpgwP3+1si+nInB7Imegfz5i9yllIUJSKgAlpRFEVRIgB+D3ww4/JfSJTTgclVLAFNV47Z1R3InjUzrnp4OksqihLeqIBWFEVRlAjCVb+jqL8gNdIldeBSR3lED7ZcOapldKBV2w546CynKEr4ogJaURRFUSIKopA33xyDTH+8hz9zyCPaGdbuUAsHMif5GBs2bnEWVBQlPFEBrSiKoigRiHsPbmLkyZ8RL7UDy+o68GCAA1c7O/BHZgcK5i8EH18fZ0lFUcILFdCKoiiKEpF4CFx8sAuNt8ZF1pYOlJ7hQL2TDjS558BM/59wzzf0QugpivJiqIBWFEVRlAjGQxHRRwIWYHlgA2y9MwKnfTfjus8F+Af6OUsoihKeqIBWFEVRFEVRlOdABbSiKIqiKIqiPAcqoBVFUZQoy/nz57F23TpJ6zVFkLRm7Tps2rQZXl5ezqukKJEPFdCKoihKlORBQADKli2LCtljY2LjXBjfKGeETOMa5TIpuPyg34OWdc0LuiyiprENcyB9/A/QpWt355VSlMiHCmhFURQlSkIBXb58eVTNGx9zWufHzJb5IlSa0TI/5rbKjRPdvsX+zgkxo4W1j8xf1jYTLvT4HKvbp8N0yWfe1o7f42af97GrcxLzfVW7dLja62Pc7B0LN/vGwvXeH+Bcj/9hyz8pMLtlXikT/HbDO01vkRdZk3yMrt16OK+UokQ+VEAriqIoUZKILqCntyiANe3TInBANDwY8AbWd0iDaZI3t1UuXOj5OTDIgdPdv8LsVnmMiN7TKREwwIFDXeMZAb2xQ0pZLzrO9fwCM1tIfZK3sE02XOr5qdQZHbs7WUI7uG2HZ1IBrUQFVEAriqIoUZKILqCZzvf4H/z7v4HbfWPCq/f7RgDv7ZwY9/u/iVt934Vf/xhY2S6DEdshCejzIrbntMxj6qOIXtEuvRHlN/vEMuI76DbDO6mAVqICKqAVRVGUKElEFtC0KK9ulw5+/WLgrIjoBa2zw6P3xyKa34NP/7ew9Z/vjXWalumT3b4xwnhPp8QhCmi6bExvWcDkH+kaBxjowNGusdUCrSivCBXQiqIoSpQkogpoito5rfLgVPevESACmEKYrhtL22bC7T7v4nCXOMYfmq4c9HGmNXpZu4zYTQEtwvhw17imjk2yHtenBdur9wfGYs3vXr0/xNr2aWRbeZ/YbkRJKqCVqIAKaEVRFCVKEhkGEdI1w3WwHy3NrlZj1zKPP1vL7e9PpifXj4hJBbQSFVABrSiKokRJIoMP9OuYVEArUQEV0IqiKEqUJDgBTT9huk8wTNyqdumxpG1m853LFrfJilXtM2Be6xzG4msLvvltsmOBJPs707zWOaVserPOLGferJZ5saRNFri1ymWswOZ72yymXIhJ9oF1ubXOZb4vlvKu2+EgwOXtMpkU0oBAhsJbJsfBwYasb3m7jMan2rZa2+X4mWm+HN9KKcPyi2T/uYyWb7ucu+wPl9n7wvqXSv3cvmt9j/ZNzqV1TjObsHv/OkZnYp3ucpwqoJWogApoRVEUJUriKqBni4CmMPbo9dH/2zu3nrjKKAynhB5sE/BASA0lLeNFVaBKqsaa0iIpf4AfYIx/QqQ1wMhhoMAQ/4ReeFFijLYoPeCxrTfFE9rEtFXbIhdFocWoLNezhl2GaTXDnZ2+T/IlM3vv7zRXz15Z35rIE57urbOPu/fYzECtzfTXhgxSveJWdqPNDj8YAopUvnd4n93MbrKF7BaX5ecjTQLhnRupsD+y5SGFXEMoqeVM6bm5Eapp5IT7uAsm5elOdTXZhb5UHAKcG660KZ/7NNe9sa7T3U9FfjO1nzkQSF9klaocv41utd9HHwjZzRdYGmv8yKU1qdrxSU+DfZ6ujzJ4yz7XtaGHYi9RbzpTE9U5uPdZT70/22gXV/KwyaFmf+Rik5O97M9d9rXwEnDi9Wft5ujmOLB4oTcV13gR4eWBdc2PbA0pn3ApT/b6/cCO2M/PQ1W+t6aVvTbZ+JFme/vVVgm0uOeRQAshhChJ1go09ZUP2o+Z7SF2/OnIpy6RXEMaQ0Y7+LOS+rg/3VcXUdVcmbnyaFcGq/y5F/1eypb9mbPpx0Ng6U/N5T/HyqJCBuXjZl2Sc5Hslci3j40kI6Y/DVXH2IX3mJdDg0SREXOEdKpnT8g7Ev1fAr3k67vm4p/ILeMh/je8H2LMiwLjcxDxrY621f4+NzK//OYGuzr0sMt7S3ynjvSlwerbAr0wuiVK6iHqHFo8/8buEGjWNT+yzY51Nq/Zz7n07pgPkb5jzYpAixJAAi2EEKIkuXsKB2kMrfb+kefs2/6dIYOI4WRXk4vdoRBGZHMpWx4R2CWX0A9daJHUxezmiKje8ms/DNTkSsch3eknI4p7KVNt4537Xcwb4vsvRx+J1IxEKosRaKLfCOwZ/07U9gsfe7EIgSZyjtwi4KyRUnaUweMZ+lzM1MT4X7roJxHzpP9Ud2NEphFo9n83gWbv131s9nPOXxx4oaAP4s0LgwRa3G9IoIUQQpQkhQJNmsZ0b8q+6quLCC9ifMUlEdGLaLKLH7JHDvBVl0Xk8LyLINe4dzb9RESefz1aYZSYQ0QpJUetZqKwX/ftsm/6d8X4/KU2KRREsHmWKHUxAn3Z11OYwkFt6GIi0NeHK2Ou/PxtWjIO6St/j22w71yu2T+R7hn/jAgTkc+lcLRFCse/CTRRdeZkXPZJ3xsSaHEfIoEWQghRkhQKNIf9kgNySU4u0sj1QskbdyGk9jICmVzjMznNSWoGQs6hOfKYGbdQXDnMRzQXeeX5Y53kOj8dB+/yn6PRn3uMn38d0Z7s2huNz/n3koa8speJrmfWrLewsQZSViZciJkr5uMA4Gstt6WYPeRyslfXwqHIk77PCf/d3ulcHT+3pwOxz0T6k/bu4RdijA8KDkXSJNCiFJBACyGEKEn+coFub2+3htpt9krbY/byoZTa/6C91Fpnj1aUWSYjgRb3LhJoIYQQQggh1oEEWgghhBBCiHUggRZCCCGEEGIdSKCFEEIIIYQoGrN/APTSLJAkj0cSAAAAAElFTkSuQmCC"
widgets.Image(value=b64decode(aeolus_meas_geometry_encoded))
Figure 1: Aeolus measurement geometry. Distance between right-most and left-most swath point is around 21 km. Image courtesy of ESA.
In order to compare collocated reference measurements with Aeolus measurements, the off-nadir intersection with the Earth’s surface is of interest.
Download orbit ground track files per FTP¶
Because the orbit files are not part of the VirES database, they must be downloaded separately via FTP connection from the ADDF server.
This option is only available for users who have the necessary access rights. Mainly these are members of Aeolus Cal/Val teams.
Defining a date for the GRND_TRACK file¶
# Date in dd.mm.yyyy
GRND_TRACK_FILE_DATE = "13.05.2020"
# separate in day, month, year
day = GRND_TRACK_FILE_DATE.split(".")[0]
month = GRND_TRACK_FILE_DATE.split(".")[1]
year = GRND_TRACK_FILE_DATE.split(".")[2]
Check if file is already available in user workspace¶
# Get user folder and set/create folder for GRND_TRACK files
user_folder = os.path.expanduser("~")
grnd_track_folder = os.path.join(user_folder, "files/GRND_TRACK")
os.makedirs(grnd_track_folder, exist_ok=True)
# Check if file for date of interest is already available
grnd_track_file_exists = False
for file in os.listdir(grnd_track_folder):
if fnmatch.fnmatch(file, "*{}{}{}*.DBL".format(year, month, day)):
grnd_track_file_path = os.path.join(grnd_track_folder, file)
grnd_track_file_exists = True
Connect to Aeolus Data Dissemination FTP server and fetch GRND_TRACK file if file is not yet in user space¶
if not grnd_track_file_exists:
# Set user and password from ESA SSO account
USERNAME = os.environ["DATAU"]
PW = os.environ["DATAP"]
# Uncomment following two lines to provide your credentials as input
# USERNAME = input("Please enter your SSO user name:")
# PW = getpass.getpass("Please enter your password:")
# Connect to the ADDF FTP server
ftp = FTP("aeolus-ds.eo.esa.int")
ftp.login(user=USERNAME, passwd=PW)
# change directory
ftp.cwd("/ADDF/Orbit_Data/{}-{}/{}/".format(year, month, day))
# get file list of directory
file_list = ftp.nlst()
# check if GRND_TRACK file is available and set file name
try:
grnd_track_file_name = [k for k in file_list if "GRND" in k][0]
except:
print("Warning: No ground track file available for this date")
assert False
# Download ground track file to user space
grnd_track_file_packed_path = os.path.join(grnd_track_folder, grnd_track_file_name)
with open(grnd_track_file_packed_path, "wb") as fp:
ftp.retrbinary("RETR " + grnd_track_file_name, fp.write)
# close FTP connection
ftp.quit()
# Extract ground track file
tar = tarfile.open(grnd_track_file_packed_path, "r:gz")
# Define grnd_track_file name for DBL-File
grnd_track_file_name_unpacked = grnd_track_file_name.split(".")[0] + ".DBL"
# Extract only the .DBL file containing the orbit predictions
tar.extract(grnd_track_file_name_unpacked, path=grnd_track_folder)
tar.close()
# Define grnd_track_file_path for DBL-File
grnd_track_file_path = os.path.join(grnd_track_folder, grnd_track_file_name_unpacked)
Define necessary functions¶
def read_grnd_track(file):
"""
Function to read Aeolus Ground Track files.
Parameters
----------
file : string
Input file path.
Returns
-------
data : dict
Aeolus orbit location for nadir and off-nadir as function of time.
"""
data = {}
date_time = os.path.basename(file)[19:34].split("T")
data["date"] = date_time[0]
data["time"] = date_time[1]
# define a function to convert date and time to datetime objects when reading the file with numpy.genfromtxt
convertfunc = lambda x: dt.datetime.strptime(x, "%Y/%m/%d-%H:%M:%S.%f")
data_raw = np.genfromtxt(
file,
skip_header=3,
dtype=None,
names="Date_time, Nadir_lat, Nadir_lon, Offpoint_lat, Offpoint_lon",
converters={"Date_time": convertfunc},
encoding='utf-8',
)
for i in data_raw.dtype.names:
data[i] = data_raw[i]
return data
def get_map(data, xlim, geo_lim, altitude_in_km):
"""
main function to process data and create leaflet map with predicted orbit locations as marker
"""
offset_in_km = convert_to_offset_in_km(altitude_in_km)
lat, lon, date_time, orbit_node = apply_filter(data, xlim, geo_lim)
lon_with_offset = get_offset(lat, lon, orbit_node, offset_in_km)
# add aditional offset because of an offset which was found between the actual measurement and the prediction
# This turned out to be a problem in the L1B product and could be solved now. So it was actually not an error in the orbit prediction.
# This line is now commented out
# lon_with_offset = add_prediction_offset(lon_with_offset, offset_in_degree=-0.07)
# get lat and lon in degrees and minutes
lat_dm, lon_dm, lon_with_offset_dm = get_coord_in_dm(lat, lon, lon_with_offset)
# plot orbit locations on leaflet map
m = plot_orbits(
lat,
lon,
lon_with_offset,
lat_dm,
lon_dm,
lon_with_offset_dm,
date_time,
offset_in_km,
)
return m
def export_orbits_as_csv(data, xlim, geo_lim, altitude_in_km):
"""
Optional export of orbits as csv-file for different ground-track offset values
corresponding to different altitudes.
"""
offset_in_km = convert_to_offset_in_km(altitude_in_km)
lat, lon, date_time, orbit_node = apply_filter(data, xlim, geo_lim)
lon_with_offset_11km = get_offset(lat, lon, orbit_node, 11)
# lon_with_offset_11km = add_prediction_offset(lon_with_offset_11km, offset_in_degree=-0.07)
lon_with_offset_21km = get_offset(lat, lon, orbit_node, 21)
# lon_with_offset_21km = add_prediction_offset(lon_with_offset_21km, offset_in_degree=-0.07)
lon_with_offset_gui = get_offset(lat, lon, orbit_node, offset_in_km)
# lon_with_offset_gui = add_prediction_offset(lon_with_offset_gui, offset_in_degree=-0.07)
time = [i.strftime("%Y/%m/%d-%H:%M:%S") for i in date_time]
file_name = "Orbit_prediction_{}.txt".format(date_time[0].strftime("%Y%m%d_%H%M"))
with open(file_name, "w") as file:
file.write(
"# Aeolus orbit prediction from {} until {} \n".format(time[0], time[-1])
+ "Offsets for 0 km, 11 km (15 km altitude), 21 km (30 km altitude) and user defined \n"
+ "# time \t lat \t lon_0km_offset \t lon_11km_offset \t lon_21km_offset \t lon_{:.2f}km_offset \n".format(
offset_in_km
)
)
for i in range(len(lat)):
file.write(
"{} \t {:.3f} \t {:.3f} \t {:.3f} \t {:.3f} \t {:.3f} \n".format(
time[i],
lat[i],
lon[i],
lon_with_offset_11km[i],
lon_with_offset_21km[i],
lon_with_offset_gui[i],
)
)
def convert_to_offset_in_km(altitude_in_km):
"""Convert altitude of Aeolus intersection into an longitudinal offset in km"""
offset_in_km = round(math.tan(math.radians(35)) * altitude_in_km, 2)
return offset_in_km
def apply_filter(data, xlim, geo_lim):
"""
apply geolocation and time filter for Orbit Ground Track File data
"""
# determine orbit node (ascending or descending)
orbit_node = determine_orbit_node(data["Offpoint_lat"])
# apply time filter and assign values to variables
lat = data["Offpoint_lat"][xlim[0]:xlim[1]]
lon = data["Offpoint_lon"][xlim[0]:xlim[1]]
date_time = data["Date_time"][xlim[0]:xlim[1]]
orbit_node = orbit_node[xlim[0]:xlim[1]]
# create additional geolocation filter mask
lat_lon_mask = (lat > geo_lim[0][0]) & (lat < geo_lim[0][1]) & (lon > geo_lim[1][0]) & (lon < geo_lim[1][1])
# apply geolocation filter mask
lat = lat[lat_lon_mask]
lon = lon[lat_lon_mask]
orbit_node = orbit_node[lat_lon_mask]
date_time = date_time[lat_lon_mask]
check_if_array_empty(lat)
return lat, lon, date_time, orbit_node
def check_if_array_empty(array):
if array.size == 0:
raise ValueError('Filters are too strict. No orbits can be found within the chosen times and geolocations.')
def determine_orbit_node(lat):
"""
determine ascending or descending node from latitude values
1 = ascending
-1 = descending
"""
orbit_node = np.full(len(lat), -1)
orbit_node[:-1][np.diff(lat) < 0] = 1
return orbit_node
def get_offset(lat, lon, orbit_node, offset_in_km):
"""
Determine longitude offset from offset in kilometre as function of latitude and orbit node.
Note that this is not reliably applicable to very high latitudes.
"""
lon_with_offset = lon + offset_in_km / (111.32 * np.cos(np.deg2rad(lat))) * orbit_node
return lon_with_offset
def add_prediction_offset(lon_with_offset, offset_in_degree):
"""
Due to an offset between the actual measurement and the predictet orbit which is under investigation,
an additional offset is necessary and can be set with this function.
This turned out to be a problem in the L1B product and could be solved now. So it was actually not an error in the orbit prediction.
This correction is no longer needed and will not be applied in the prediction.
"""
lon_with_offset = lon_with_offset + offset_in_degree
return lon_with_offset
def plot_orbits(lat, lon, lon_w_offset, lat_dm, lon_dm, lon_with_offset_dm, date_time, offset_in_km):
"""
Create leaflet map and plot orbit locations as markers
"""
# create string representation of times
time = [i.strftime("%a %Y/%m/%d-%H:%M:%S") for i in date_time]
# determine center of map depending on geolocations to plot
map_center_lat = lat.min() + (lat.max() - lat.min()) / 2.0
map_center_lon = lon.min() + (lon.max() - lon.min()) / 2.0
# geolocations as strings to show in marker message
lat_dm_str = ["{:d}° {:.2f}' N".format(i[0], i[1]) for i in lat_dm]
lon_dm_str = ["{:d}° {:.2f}' E".format(i[0], i[1]) for i in lon_dm]
lon_with_offset_dm_str = ["{:d}° {:.2f}' E".format(i[0], i[1]) for i in lon_with_offset_dm]
# create leaflet map
m = Map(
center=[map_center_lat, map_center_lon],
zoom=2,
dragging=True,
scroll_wheel_zoom=True,
)
for j, i in enumerate(zip(lat, lon, lon_w_offset, lat_dm_str, lon_dm_str, lon_with_offset_dm_str)):
# leaflet marker
new_marker = Marker(location=(i[0], i[2]), draggable=False)
message = widgets.HTML()
# popup message to show when marker is clicked
message.value = (
"Lat: {:.3f} Lon: {:.3f} <br>"
+ "Lat: {} Lon: {} <br>"
+ "Lon with {:.2f} km offset from ground track <br>"
+ "Time: {} UTC"
).format(i[0], i[2], i[3], i[5], offset_in_km, time[j])
new_marker.popup = message
m.add_layer(new_marker)
# add controls to map
m.add_control(LayersControl())
measure = MeasureControl(position="bottomleft", active_color="orange", primary_length_unit="kilometers")
m.add_control(measure)
measure.completed_color = "red"
# map height
m.layout.height = "600px"
return m
def determine_axis_limits(data):
'''Get axis limits and string represenation of time for the GUI'''
x_lim = [(i.strftime("%Y/%m/%d-%H:%M:%S"), j) for j, i in enumerate(data["Date_time"])]
return x_lim
def decimaldegree_to_dms(deg):
'''Convert decimal degrees to degrees minutes and secons'''
f, d = math.modf(deg)
s, m = math.modf(abs(f) * 60)
return (int(d), int(m), s * 60)
def decimaldegree_to_dm(deg):
'''Convert decimal degrees to degrees and decimal minutes'''
f, d = math.modf(deg)
return (int(d), abs(f) * 60)
def get_coord_in_dms(lat, lon, lon_with_offset):
'''Convert an array or list of coordinates from decimal degrees to degrees minutes and seconds'''
lat_dms = [decimaldegree_to_dms(i) for i in lat]
lon_dms = [decimaldegree_to_dms(i) for i in lon]
lon_with_offset_dms = [decimaldegree_to_dms(i) for i in lon_with_offset]
return lat_dms, lon_dms, lon_with_offset_dms
def get_coord_in_dm(lat, lon, lon_with_offset):
'''Convert an array or list of coordinates from decimal degrees to degrees and decimal minutes'''
lat_dm = [decimaldegree_to_dm(i) for i in lat]
lon_dm = [decimaldegree_to_dm(i) for i in lon]
lon_with_offset_dm = [decimaldegree_to_dm(i) for i in lon_with_offset]
return lat_dm, lon_dm, lon_with_offset_dm
Search for available GRND_TRACK files in user space (must be downloaded first per FTP)¶
Orbit_Grnd_Track_files = [('0000', '0')]
for root, dirs, files in os.walk(grnd_track_folder):
for name in sorted(files):
if fnmatch.fnmatch(name, '*GRND_TRACK*.DBL'):
Orbit_Grnd_Track_files.append((name, os.path.join(root, name)))
Define geolocation, time, altitude to create leaflet map with orbit data¶
As an alternative a GUI is created in the next cell where you can choose between different files which are already in your user space. You just need to uncomment the code.
# geolocation
# lat between -90 and 90
lat_min = 40
lat_max = 55
# lon between -180 and 180
lon_min = 5
lon_max = 20
# please choose a time within 7 days of the chosen GRND_TRACK_FILE_DATE in following format: YYYY/MM/DD-HH:MM:SS
time_min = "2020/05/15-00:00:00"
time_max = "2020/05/20-00:00:00"
# altitude of the measurement - geolocation differs due to the 35 degree off-nadir angle
altitude_in_km = 12
orbit_grnd_track_data = read_grnd_track(grnd_track_file_path)
xlim_min = np.argmin(
np.abs(orbit_grnd_track_data["Date_time"] - dt.datetime.strptime(time_min, "%Y/%m/%d-%H:%M:%S"))
)
xlim_max = np.argmin(
np.abs(orbit_grnd_track_data["Date_time"] - dt.datetime.strptime(time_max, "%Y/%m/%d-%H:%M:%S"))
)
leaflet_map = get_map(
data=orbit_grnd_track_data,
xlim=(xlim_min, xlim_max),
geo_lim=((lat_min, lat_max), (lon_min, lon_max)),
altitude_in_km=altitude_in_km,
)
Create graphical user interface¶
Please uncomment the following cell if you want to use a GUI for the selection of the orbit ground track data
# filelist = widgets.Dropdown(
# options=sorted(Orbit_Grnd_Track_files),
# # value=sorted(Orbit_Grnd_Track_files)[0],
# description="File:",
# disabled=False,
# )
# output = widgets.Output()
# clear_button = widgets.Button(description="Clear Loaded Files")
# plot_button = widgets.Button(description="Plot Data")
# export_button = widgets.Button(description="Export Data")
# file_list_text = widgets.HTML(
# description="Loaded Files:",
# )
# loaded_files = {"0000": "00"}
# selected_data = {}
# selected_file = widgets.Dropdown(
# options=loaded_files,
# description="Selected File:",
# disabled=False,
# )
# set_xlim_min = widgets.SelectionSlider(
# options=[0, 1, 2, 3, 4, 5],
# description="xlim_min:",
# disabled=False,
# layout={"width": "500px"},
# )
# set_xlim_max = widgets.SelectionSlider(
# options=[0, 1, 2, 3, 4, 5],
# description="xlim_max:",
# disabled=False,
# layout={"width": "500px"},
# )
# set_geolocation_lat = widgets.IntRangeSlider(
# value=(40, 55),
# min=-90,
# max=90,
# description="latitude range:",
# disabled=False,
# layout={"width": "500px"},
# style={"description_width": "initial"},
# )
# set_geolocation_lon = widgets.IntRangeSlider(
# value=(5, 20),
# min=-180,
# max=180,
# description="longitude range:",
# disabled=False,
# layout={"width": "500px"},
# style={"description_width": "initial"},
# )
# set_offset = widgets.BoundedIntText(
# description="Altitude where to intersect with Aeolus",
# value=12,
# min=0,
# max=30,
# layout={"width": "500px"},
# style={"description_width": "initial"},
# )
# def on_clear_button_clicked(b):
# global loaded_files
# loaded_files = {"0000": "0"}
# file_list_text.value = ""
# def on_plot_button_clicked(b):
# global leaflet_map
# leaflet_map = get_map(
# data=selected_data,
# xlim=(set_xlim_min.value, set_xlim_max.value),
# geo_lim=(set_geolocation_lat.value, set_geolocation_lon.value),
# altitude_in_km=set_offset.value,
# )
# with output:
# print("Map available")
# def on_csv_export_button_clicked(b):
# export_orbits_as_csv(
# data=selected_data,
# xlim=(set_xlim_min.value, set_xlim_max.value),
# geo_lim=(set_geolocation_lat.value, set_geolocation_lon.value),
# altitude_in_km=set_offset.value,
# )
# def handle_filelist_selection(select):
# global loaded_files
# data = read_grnd_track(select.new)
# data_key = data["date"] + "_" + data["time"]
# loaded_files[data_key] = data
# file_list_text.value = "<br>".join(list(loaded_files.keys()))
# selected_file.options = sorted(loaded_files)
# def handle_file_selection(select):
# global selected_data
# selected_data = loaded_files[select.new]
# xlim = determine_axis_limits(selected_data)
# set_xlim_min.options = xlim
# set_xlim_max.options = xlim
# set_xlim_min.value = xlim[0][1]
# set_xlim_max.value = xlim[-1][1]
# # Connect widgets and functions
# filelist.observe(handle_filelist_selection, names="value")
# clear_button.on_click(on_clear_button_clicked)
# selected_file.observe(handle_file_selection, names="value")
# plot_button.on_click(on_plot_button_clicked)
# export_button.on_click(on_csv_export_button_clicked)
# # Layout
# leftbox = widgets.VBox(
# [
# filelist,
# clear_button,
# selected_file,
# set_xlim_min,
# set_xlim_max,
# set_geolocation_lat,
# set_geolocation_lon,
# set_offset,
# plot_button,
# export_button,
# output,
# ]
# )
# widgets.HBox([leftbox, file_list_text])
# If Plot-button was pressed, wait if "map is available" and execute this cell to show the map.
leaflet_map